Reference no: EM132937880
1. QUESTION Consider the following statements. Indicate for each of them if they describe a Damage (D), a Risk (R), a Hazard (H) or Availability (A).
|
REQUIREMENT
|
TYPE (D/R/H/A)
|
|
Cost estimated for the environmental recovery in case of tank leakage is 500 €/y
|
|
|
Submersible pumps must be extracted from the tank, by crane, for maintenance once a year
|
|
|
The loss of production expected, due to failures, is 40.000 €/y
|
|
|
In case of tank leakage, the deep of pollution into the ground is 40 cm
|
|
|
The cost for the repair of pump P4 is 2500 €
|
|
2. QUESTION
Given the following TOP cut set expression:
TOP= A • C + A • B • C + C • D "•" = AND
"+" = OR
Consider all the failure modes as "Repairable when failed"
What is the event requiring the stronger improvement in terms of availability in order to increase the overall availability of the system?
A
B
C
D
Describe the motivation of your choice
3. QUESTION
Consider the Reliability Block Diagram in the figure, write the TOP EVENT expression as union of Minimal Cut Sets:
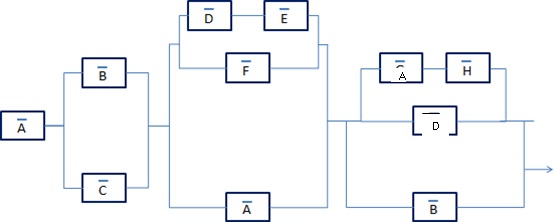
TOP =
...
Now, considering that K1 and K2 are Common Cause Failures joining all the events, rewrite the final expression including the CCF:
Estimate P(TOP) using the Beta factor approach (β = 5%), supposing that P(A)=P(B)=P(C)=...=P(H)= 10-3
4. QUESTION
Draw the simplest Fault Tree corresponding to the RBD analysed in the previous exercise, including CCFs:

5. QUESTION
You plan to throw two dice contemporary. Consider the following events: A: the outcome of the first die is 5
B: the sum of the two outcomes is equal or higher than 9 C: the sum of the two outcomes odd (dispari)
Select the correct relationships:
|
Events
|
Are dependent
|
Are independent
|
Are Mutually Exclusive
|
|
A, B
|
|
|
|
|
A, C
|
|
|
|
|
B, C
|
|
|
|
Estimate the probability of the following expressions:
P(A and B) = ................. P(B and C) = ...........................
P ((A or C) and B) = .....................................
6. DOMANDA (PUNTI: 4/48)
Consider a tank of gasoline (a vertical cylinder with a internal diameter of 1,5 m). Pressure inside the tank is the atmospheric pressure and Temperature is 15 °C. At these conditions, gasoline is liquid.
Gasoline density is 700 kg/m3 and the height of liquid level inside is H=4 m (measured form the floor of the tank).
Assume a rupture in the tank (circular hole) at an height of 2,5 m from the floor, the diameter of the hole is 15mm and CD = 0.8.
Please answer the following questions:
Is the mass flow rate coming out form the hole changing in time or is it constant in time? (CHANGING/CONSTANT) : ..............................
What is the maximum flow rate coming out from the hole? (kg/s)
What is the time of the transient corresponding at the maximum flow rate (consider time 0 the beginning of the release)? (s)
What is the total amount of gasoline that will be released from the tank? (kg)
If you fix the total volume of the tank, in your opinion, is the emptying of the tank faster in case of small diameter and big height or in case of big diameter and small height (answer here below and provide a justification of your answer)?
7. QUESTION
Consider the two fire fighting systems shown in the following figures.
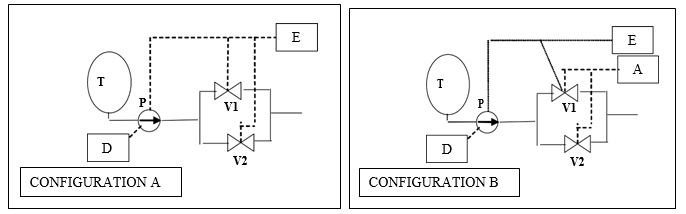
Consider the success criteria (requirement) "intervention on demand in case of fire". Suppose that:
» One valve line is sufficient to provide the nominal flow
» Pump can be fed by electrical power (E) or by the diesel engine (D)
» In configuration A both valves are fed by electrical power (E),
» In configuration B both valves are fed by instrument air (A) but V1 can be opened also by electrical power (E)
» Assume that the probability of each failure is 10-3, i.e. P(A)=P(E)=P(T)=....=10-3
Write the MCS expression for the two configurations:
TOP A: .....................................................
TOP B: .....................................................
Which is the best configuration in terms of probability of success of the system?
- Configuration A
- Configuration B
Because (explain the motivation of your choice):
8. QUESTION
Consider the following sentences and indicate if they are TRUE or FALSE.
SENTENCE TRUE/FALSE
Wind direction and intensity can change shape and dimension of the damage area of a pool fire
In case of a continuous accidental release of a pressurised flammable gas into the atmosphere, if the mix gas-air is immediately ignited, the resulting phenomena is a flash fire
BLEVE is a chemical explosion
The dispersion of a gas cloud in the atmosphere is depending on the gas density
Consider a plant where a potential fire can produces a High Lethality Area with a radius of 20 m. Firefighting pumps can be installed in this area without any particular protection but the diesel storage feeding the pumps must be installed outside this High Lethality Area or in alternative must be protected by a fire wall.
In case of catastrophic rupture of a vessel containing propane, a fireball phenomenon is expected.
9. QUESTION
Consider a Hydrogen pressurised gas storage on ground. The content of the storage is 5000 kg.
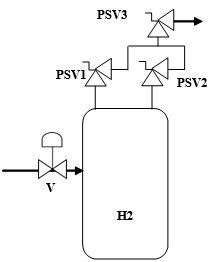
The storage is equipped by a control valve V to regulate the pressure inside the tank and 3 Pressure Safety Valves PSVs, as reported in the following figure:
The components are characterised by the following failure modes:
|
Component
|
Failure Mode
|
Failure Rate (1/h)
|
Repair rate (1/h)
|
Time necessary to
perform test(τ0)
|
|
Control valve
|
Spurious position
|
5 x 10-5
|
10-1
|
negligible
|
|
Control valve
|
Leakage
|
1 x 10-5
|
10-1
|
negligible
|
|
PSV
|
Stuck closed
|
1 x 10-6
|
10-1
|
negligible
|
|
PSV
|
Leakage
|
1 x 10-4
|
10-1
|
negligible
|
The system is tested every 1000 hours.
PSV1 and PSV2 are redundant, one of them is able to guarantee the overpressure discharge.
You have to estimate the frequency of occurrence (ev/y) of the failure of control valve, supposing that this failure is able to produce an over pressure inside the storage (this will be the Initiating Event to be considered for the following steps).
Write the equation for this evaluation:
Equation - fIE = ...............................................
Calculate the result
Result - fIE = [ev/y]
After that, it is necessary the estimation of the frequency of the explosion due to overpressure of the storage in case of the control valve and PSVs failure (explosion scenario).
Equation - fscen = ...............................................
Calculate the result
Result - fscen = [ev/y]
Suppose now that there is a common cause failure among PSVs, i.e. the maintenance error, characterised by β=10%.
The new result considering CCF is - fscen = [ev/y]
Now, consider the normal operation of the system, without any error in regulation.
What is the frequency of occurrence of a H2 release due to componet leakages?
Draw the RBD for the TOP: "H2 Leakage"
Write the TOP EVENT in terms of MCSs:
TOP = ...........................................................
Write the equation:
F leak (ev/y) = ..............................................................................................................................
Write the numerical result
F leak (ev/y) = ...........................................................................
Attachment:- Risk Analysis with consequences.rar