Reference no: EM131403181
Assignment: Probability
Abstract: You will implement several Bayesian networks and sampling algorithms to gain a better understanding of probabilistic systems.
Learning Objectives: Students should be able to understand the importance of Bayesian networks to represent conditional dependencies. Also, be able learn the sampling methods, Gibbs and Metropolis-Hastings and develop an intuition for their convergence criteria (very "researchy").
Evaluation: Evaluation is using the last submission on Bonnie.
The Challenge -
Many AI systems rely on probabilistic knowledge of the world, rather than absolute knowledge, to execute tasks efficiently: for example, motion planning in robots with unreliable sensors. One type of probabilistic system that is especially useful is the Bayesian network, which encodes a joint probability distribution among dependent variables as a network of conditional probabilities. Your challenge is to implement and test several of these networks, ultimately using a sampling method to approximate a probability distribution.
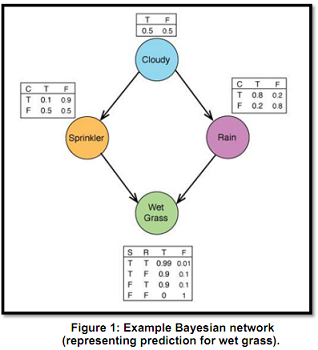
Your Assignment -
Your task is to implement a few basic networks as well as several sampling algorithms. You will do this in probability notebook.ipynb, and there are tests along the way to help. Unlike previous assignments, we will not be grading on performance but rather on completion.
We have provided the following additional classes and files: (GitHub Repo):
|
File/Folder
|
Description
|
|
Probability_tests.py
|
To test the models you've built.
|
|
Pbnt/combined
|
Module to implement Bayesian networks (you'll basically need BayesNode in Node.py and BayeNet in Graph.py).
Also contains an example (ExampleModels.py) to help you get started.
|
This is meant to be a shorter assignment, so there won't be much testing required.
Attachment:- Assignment File.rar
|
Insulating solid sphere of radius
: An insulating solid sphere of radius R has a non-uniform charge density that varies with r according to the expression ρ = Ar2 where A is a constant and r R
|
|
State the hypothesis in terms of the parameter of the model
: The researcher hypothesized that dance/ movement therapists with more years in formal dance training will report higher perceived success rates in cotherapy relationships. State the hypothesis in terms of the parameter of the model, part a.
|
|
What is the maximum current across the resistor
: A 8.0-nF capacitor with an initial charge of 10 mC is discharged through a 5-kΩ resistor. (a) Calculate the current in the resistor 2 μs after the resistor is connected across the terminals of the capacitor. (b) What charge remains across the capa..
|
|
Find the least squares estimates of the intercept and slope
: Find the least squares estimates of the intercept and slope. Interpret them.- Use a 95% confidence interval to estimate the slope β1. Interpret the interval in terms of this application.
|
|
Task - implement a few basic networks
: CS 3600 Assignment: Probability. Your task is to implement a few basic networks as well as several sampling algorithms. You will do this in probability notebook.ipynb, and there are tests along the way to help. Unlike previous assignments
|
|
Temperature changes from 0oc to 100oc
: What is the fractional change in the resistance of an iron filament when its temperature changes from 0oC to 100oC?
|
|
Magnitude and direction of the electric field
: The potential in a region between x = 0 and x = 10.0 m is V = b + mx, where b = 20.0 V and m = -6.00 V/m. Find (a) the potential at x = 0, 2.00 m and 5 m and (b) determine the magnitude and direction of the electric field at x = 0, 2.00 m and 5.00..
|
|
How does income or loss compare to original income statement
: Consequently, you will not need all the accounts listed above. How does the income or loss compare to the original income statement? Explain the importance of the matching concept.
|
|
Expression for the electric field
: Over a certain region of space, the electric potential is V =5x - 3x2y + 2yz2. Find (a) an expression for the electric field (b) the magnitude of the electric field at the point (4, 0, -3).
|