Replace the previous heuristic with the manhattan distance

Assignment Help Python Programming

Reference no: EM132263058

Assignment -

Question - A* - Sliding Tile Puzzle

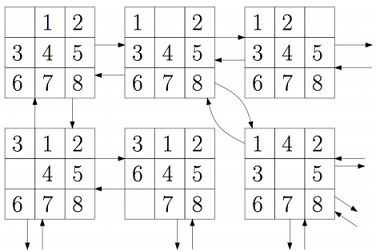
The sliding tile puzzle is a simple toy that consists of a number of tiles, and an empty space that can be used to move tiles around. The sliding tile puzzle defines a graph, where each state of the puzzle is a vertex, and there are edges between states if they can be reached by a single move:

We can define the planning problem as a search problem by giving:

An initial state.
A goal state
A set of operators that define how to create states from other states.

A deterministic plan is a sequence of actions to achieve a goal from a given starting state. A deterministic planner is a problem solver that can produce a plan. The Input is an initial state and description, a specification of the actions available to the system, and a goal description. The specification of the actions includes their preconditions and their effects.

In this assignment , you will implement a program that uses A* search to solve the Eight Puzzle game. Your program will take an initial board position, and then try to find a sequence of moves from the initial position to the goal position. Moves are represented by moving the black space left, right, up, or down.

Manhattan distance: this heuristic is used for its simplicity and also because it underestimate (i.e., lower bound) on the number of moves required to bring a given board to the solution board. We simply compute the sum of distances of each tile from where it belongs, completely ignoring all other tiles.

Important: to implement your search algorithm, you will need to:

Implement an open list, that allows you to add a state /priority pair and remove the pair with the smallest priority.
Implement a closed list, that allows you to add a state, and check if a state is in the closed list.
Implement a search state, that allows you to compare two states, find the estimated cost from one state to another, and generate all children of a given search state.

Exercise:

Implement the A* algorithm using the number of misplaced tiles as a heuristic function.
Replace the previous heuristic with the manhattan distance.

Question - Blackbox planner

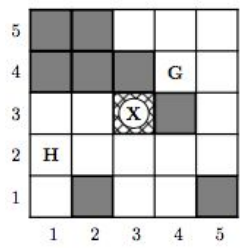
Hansel and Gretel are lost in a rectangular forest. Even worse, they are separated from each other. Fortunately, there is the friendly neighborhood witch who is willing to help them reunite. As an appropriate place for the meeting she proposes her gingerbread house in the middle of the forest.

Hansel and Gretel can both move in four directions, namely north, east, south and west. Call the actions northH , southH, eastH, westH, northG, southG, eastG, and westG, respectively, with the obvious semantics of moving either Hansel or Gretel by one grid cell in the indicated direction. Some cells with extremely thick vegetation are inaccessible (shown in grey in the figure below) and cannot be moved to. The goal is to move both Hansel and Gretel to the goal position in the center of the grid, marked by X. Their current positions are indicated by H and G, respectively.

Exercise:

Solve the problem (and help Hansel and Gretel) using PDDL and the blackbox solver.

You need to create two separate files (domain file and problem file).

The deliverable of this project will consists of a python code and PDDL files.

Attachment:- Assignment File.rar

Reference no: EM132263058

Questions Cloud

Evaluate the relative value of each organization services : Identify four organizations in a community that deliver primary health care. These must be 4 different organizations and not one agency offering 4 different.

What is the firm probable perfect-order performance : What is the firm’s probable perfect-order performance?

What are the main policy tools the federal reserve : 1. What are the main policy tools the Federal Reserve of the United States can use to control the money supply. Briefly describe each tool.

What is an organic organization : What is an organic organization? A mechanistic organization? How does the environment influence organic and mechanistic structures?

Replace the previous heuristic with the manhattan distance : Implement the A* algorithm using the number of misplaced tiles as a heuristic function. Replace the previous heuristic with the manhattan distance

Which one would you recommend to sally : Find out the approximate historical average, lowest, and highest volatility from the Telstar's volatility graph.

High-technology manufacturing activity : Why do you think China is now a favored location for so much high-technology manufacturing activity?

Argument that free trade is beneficial : What are the implications of this observation for the argument that free trade is beneficial?

What impact does have on firm perfect-order performance : Suppose the firm’s performance on two of the 95-percent factors falls to 90 percent. What impact does this have on the firm’s perfect-order performance?

User Account

All Pages