Reference no: EM132250208

Mathematical Expression and Reasoning for Computer Science Assignment -

Question 1 - Induction and sequences

Consider the following definition of a sequence of numbers:

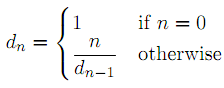
For example, d₀ = 1, d₁ = 1, d₂ = 2, d₃ = 3/2, and d₄ = 8/3. Our goal is to prove the following statement: "For all natural numbers n, d_n > √n if and only if n is even."

Complete the following two proofs, which together will prove the above statement.

(a) Prove the following using induction: ∀n ∈ Z⁺, d_2n-1 ≤ √(2n - 1).

Hints: in the induction step, write d_2k+1 in terms of d_2k-1 using the given definition of the sequence. Later as an intermediate step, use difference of squares: (2k - 1)(2k + 1) = 4k² - 1.

(b) Prove the following (with or without using induction): ∀n ∈ N, d_2n > √(2n).

You may use the statement you proved in part (a) in this part.

Question 2 - Number Representations

As you might suspect, it is possible to represent numbers in other ways besides decimal (base-10) and binary (base-2). One intriguing representation is balanced ternary.

In balanced ternary, numbers are represented as sequences of digits (d_k-1d_k-2 · · · d₁d₀)_bt, where each digit d_i is T, 0, or 1, with "T" used to represent the value -1. The value of sequence (d_k-1d_k-2 · · · d₁d₀)_bt is then simply _i=0Σ^k-1d_i × 3ⁱ.

For example, (T01)_bt represents the number (-1) × 3² + 0 × 3¹ + 1 × 3⁰ = -9 + 1 = -8.

(a) (i) Write the decimal value of the balanced ternary number (T011T)_bt.

(ii) Write the balanced ternary representation of the decimal number 210 that doesn't have any leading zeroes.

(b) Prove using induction that ∀n ∈ Z⁺, 6|3ⁿ - 3.

(c) Let x ∈ N and n ∈ Z⁺. We say that x is n-digit positively balanced if and only if it has a balanced ternary representation (d_n-1d_n-2 · · · d₁d₀)_bt in which none of the digits are equal to T. For example, the decimal number 31 is 4-digit positively balanced, with the representation (1011)_bt, and it also is 6-digit positively balanced, with the representation (001011)_bt.

Prove, by induction, the following statement:

∀n ∈ Z⁺, ∀x ∈ N, (x is n-digit positively balanced) ⇒ 6 | x - 2 ∧ 6 | x - 5

You may use part (b) and the Quotient-Remainder Theorem (QRT) in this question.

Question 3 - Properties of Asymptotic Notation

Prove or disprove each of the following statements.

You may use the "max", ceiling, and floor functions in your solutions. However, you may not use any external facts of Big-Oh/Omega/Theta, and instead should only be using their definitions in your proofs.

The following definitions apply to part (d).

Definition 1 (non-decreasing). Let f : N → R^≥0. We say that f is non-decreasing if and only if for all x, y ∈ N, if x ≤ y then f(x) ≤ f(y) (note that f(x) and f(y) can be equal).

Definition 2 (power of two). Let n ∈ N. We say that n is a power of two if and only if there exists a k ∈ N such that n = 2^k.

Note - Need Only Question 3.

Attachment:- Assignment File.rar