Reference no: EM131834423
The amount of bread (in hundreds of pounds) that a certain bakery is able to sell in a day is found to be a numerical-valued random phenomenon, with a probability function specified by the probability density function (), given by
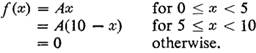
(i) Find the value of A which makes f(.) a probability density function.
(ii) Graph the probability density function.
(iii) What is the probability that the number of pounds of bread that will be sold tomorrow is (a) more than 500 pounds, (b) less than 500 pounds, (c) between 250 and 750 pounds?
(iv) Denote, respectively, by A, B, and C, the events that the number of pounds of bread sold in a day is (a) greater than 500 pounds, (b) less than 500 pounds, (c) between 250 and 750 pounds. Find P[A I B], P[A | C]. Are A and B independent events? Are A and C independent events?
|
Define types of hazards addressed by industrial hygienists
: Define the types of hazards addressed by industrial hygienists. Discuss the types of control methods used by industrial hygienists.
|
|
Independent random variables
: In exercises let X and Y be independent random variables. Let U = X + Y and V = Y - X. Let A = [|V| = 1]. Find (i) p[A|U = 1], (ii) FV|U(0|1)
|
|
Find the probability for k
: Consider the events A and B defined in example lA. Assuming that P[A] = P[B] = ½, P[AB] = 1/3, find the probability for k = 0, 1,2, that (i) exactly k
|
|
Discuss strategies that information security can use
: Discuss strategies that information security professionals can use in their unregulated organizations to motivate company executives.
|
|
Numerical-valued random phenomenon
: The amount of bread (in hundreds of pounds) that a certain bakery is able to sell in a day is found to be a numerical-valued random phenomenon
|
|
Identify the failures in process and design
: Evaluate which of the security principles you covered in Unit 1 were violated throughout these activities to set up and manage his network.
|
|
Describe a procedure for forming a random sample
: Using this result, describe a procedure for forming a random sample of a random variable with a X2 distribution with 2n degrees of freedom.
|
|
Independent random variables
: Let X and Y be independent random variables, each exponentially distributed with parameter A. Find the probability density function of Z = X1(X + Y).
|
|
Independent identically distributed random variables
: Show that if X1, X2 , ............... ,Xn are independent identically distributed random variables, whose minimum Y = minimum
|