Reference no: EM1337237
Module FEA - FINITE ELEMENT ANALYSIS
Question 2/ Method to assess the value of your analysis output
a) What is the characteristic of the system matrix of a FEA analysis? Which information can you extract from the pivot ratio?
b) Through three reasons discuss the possible errors occurred by un-correct loading.
c) Give three reasons for which non-linear FEA is required when not expected.
d) Which tools does Ansys propose to estimate errors? Give brief explanation and provide the command line for the three of them?
e) Discuss linear and parabolic elements within their application. Which one of linear or parabolic elements would you use for highly curved geometries? Explain why.
f) What is a discretisation error? What is a formulation error? What is a numerical error?
Question 3/ Thermal analysis
Problem description
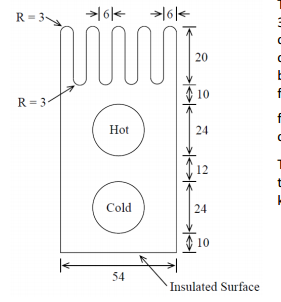
The heat exchanger shown below is used to cool a motor. The coolant coming from the motor (hot fluid) runs through the block near a cold fluid coming from a separate reservoir. The base of the heat exchanger is mounted on an insulated surface (no heat transfer occurs across the base). The heat exchanger also utilizes fins along its top surface to increase heat transfer to the surrounding air through convection.
As shown in the figure below, the heat exchanger block is 54 mm wide by 80 mm high, and is sufficiently long that it can be analysed using a 2D thermal analysis; i.e., heat flow in the third direction (into the paper) can be neglected. The five fins on the top surface are 6 mm thick, with 6 mm spacing between fins, rounded on the inner and outer edges with a 3 mm radius. The fins are 20 mm long. Both fluid channels have a diameter of 24 mm and are centred horizontally in the block.
The air temperature surrounding the heat exchanger is 300 K, and the convective heat transfer (film) coefficient can be assumed to be h = 400 W/m2-K. This convection acts on all external surfaces except for the base, which is insulated. The temperature of the hot fluid is T hot = 600 K, and the temperature of the cold fluid is Tcold = 285 K. The convective heat transfer coefficient of both fluids is h = 5000 W/m2-K.
The heat exchanger is made of an aluminium alloy with the following thermal properties (density, ρ = 2702 kg/m3):
Temperature (K) 200 300 400 600
Thermal Conductivity, k (W/m-K) 237 237 240 231
Specific Heat, c (J/kg-K) 798 903 949 1033
Assume an initial temperature for the heat exchanger of 300 K. Assume the thermal loads (convections) are applied suddenly (stepped).
a) Build an appropriate finite element model of the heat conduction problem using Ansys and provide a complete set of command lines. The text file should contain three set of commands: heading, pre-processor, and solve.
b) Justify the type and the dimension of element you have chosen.
Perform a transient thermal analysis of the heat exchanger from which you will determine the temperature distribution in the exchanger after 2 minutes, and generate temperature vs. time plots for the hottest and coolest nodes in the heat exchanger, as well as the node at the top of the centre fin.
c) Plot a nodal temperature plot after 2 minutes of the heat exchanger, and a temperature vs. time plot for the nodes listed above. Three plots should be provided.
d) Determine the length of time for the hottest node to reach 440 degree Kelvin.
e) Has the temperature of the heat exchanger reached steady-state conditions after 2 minutes?
f) List the nonlinear solution parameters used in the analysis (i.e.: time step size, and max and min values if automatic time stepping was used).
Question 4 PZT actuator
a) Using the code below model a PZT actuated composite beam.
b) Using the ANSYS help file Mechanical APDL-Command Reference lightly comment the supplied code
c) Solve the static model and extract the maximum tip deflection and plot stress
d) Using a suitable frequency range extract 3 resonant modes
e) Using the same geometry & inputs how could the tip deflection be increased
FINISH
/CLEAR
/PREP7
/UNITS, SI
um=1e-6
eps_0=8.854e-12
dens_p=7700
c11_p=1.57e11
c12_p=1.09e11
c13_p=9.77e10
c33_p=1.23e11
c44_p=2.57e10
e31_p=-1.93
e33_p=15.5
e24_p=10.81
eps11_p=1370*eps_0
eps33_p=1500*eps_0
damp_pzt=1.0e-3
loss_pzt=0.013
dens_s=2330
young_s=160e9
poiss_s=0.23
damp_si=1.0e-5
beam_dn=2
piez_dn=1
meshsize=25*um
beam_w=75*um
beam_l=350*um
beam_t=10*um
piez_t=2*um
ET, 1, PLANE42
ET, 2, SOLID186
ET, 3, SOLID5
MP, EX, 1, young_s
MP, DENS, 1, dens_s
MP, NUXY, 1, poiss_s
MP, DMPR,1,damp_si
MP, DENS, 2, dens_p
MP,DMPR,2,damp_pzt
TB, ANEL, 2
TBDATA, 1, c11_p
TBDATA, 2, c12_p
TBDATA, 3, c13_p
TBDATA, 7, c11_p
TBDATA, 8, c13_p
TBDATA, 12, c33_p
TBDATA, 16, (c11_p-c12_p)/2
TBDATA, 19, c44_p
TBDATA, 21, c44_p
TB, PIEZ, 2
TBDATA, 3, e31_p
TBDATA, 6, e31_p
TBDATA, 9, e33_p
TBDATA, 14, e24_p
TBDATA, 16, e24_p
MP, PERX, 2, eps11_p
MP, PERY, 2, eps11_p
MP, PERZ, 2, eps33_p
RECTNG, 0, beam_l, 0, beam_w
ESIZE, meshsize
MSHAPE,0,2D
AMESH, ALL
TYPE, 2
MAT,1
ESIZE, , beam_dn
VEXT, ALL, , , , , -beam_t
TYPE, 3
MAT, 2
ESIZE, , piez_dn
ASEL, , LOC, Z, 0,1e-11
VEXT, ALL, , , , , piez_t
ALLSEL, ALL
NSEL,S, LOC, z, 0,1E-11
*GET,node_o,NODE,,NUM,MIN
CM,out,NODE
CP, NEXT, VOLT, ALL
D,node_o, VOLT, 0
NSEL,S , LOC, z, piez_t, piez_t+1.0E-11
*GET,node_s,NODE,,NUM,MIN
CM,signal,NODE
CP, NEXT, VOLT, ALL
D,node_s, VOLT, 5
NSEL,S,LOC, X, 0, 1e-11
D, ALL, UX, 0
D, ALL, UY, 0
D, ALL, UZ, 0