Find the inverse transformation

Assignment Help Applied Statistics

Reference no: EM132312162

Assignment - Elements of Probability

Q1. Consider two random variables X and Y with the joint probability density

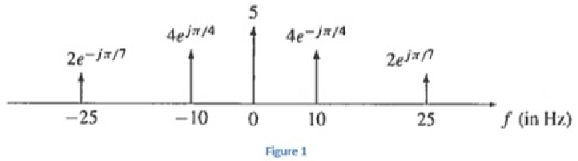
Let Z = XY² and W = Y be a joint transformation of (X, Y).

(a) Find the support of (Z, W).

(b) Find the inverse transformation.

(d) Find the joint pdf of (Z, W).

(e) Find the pdf of Z = XY² from the joint pdf of (Z, W).

Q2. Let X₁, X₂, · · · , X_n be a random sample of size n from a geometric distribution with pmf

f(x) = 0.75 · 0.25^x-1, x =1, 2, 3, · · · .

(a) Find the mgf M_{Y_3}(t) of Y₃ = X₁ +X₂ +X₃ using the geometric mgf. Then name the distribution of Y₃.

(b) Find the mgf M_{Y_n}(t) of Y_n = X₁ +X₂ + · · · + X_n. Then name the distribution of Y_n.

(d) Find the limit lim_n→∞M_{Y¯_n}(t) using the result of (c). What distribution does the limiting mgf correspond to?

(e) Let Z_n = 3/2√n Y¯_n - 2√n. Find M_{Z_n}(t), the mgf of Z_n. Then ?nd the limiting mgf lim_n→∞M_{Z_n}(t). What is the limiting distribution of Z_n?

Q3. Consider two random variables X and Y with the joint probability density

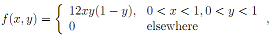
which is the same as in Question 1. Now let Z = XY²and U = X be a joint transformation of (X, Y).

(a) Find the support of (Z, U).

(b) Find the inverse transformation.

(d) Find the joint pdf of (Z, U).

(e) Find the pdf of Z = XY² from the joint pdf of (Z, U).

Q4. Let X₁, X₂ and X₃ be a random sample (i.e. X₁, X₂, X₃ are independent) of size n =3 from the exponential distribution with pdf f(x)= ½e^-x/2, 0 < x < ∞. Find

(a) P(1 <X₁ < 2, 2 < X₂ < 3, 3 < X₃ < 4).

(b) E[X₁X₂²(X₃ - 2)²].

Q5. Let X₁, X₂, X₃ denote a random sample of size n =3 from a distribution with the Poisson pmf

f(x)= (2^x/x!)e^-2, x = 0, 1, 2, 3 · · · .

(a) Compute P(X₁ + X₂ + X₃ =1).

(b) Find the moment-generating function of Z = X₁ +X₂ +X₃ using the Poisson mgf of X₁. Then name the distribution of Z.

(d) If Y =max{X₁, X₂, X₃}. Find the probability P(Y ≤ 2).

Q6. If E(X) = 16 and E(X²) = 292, use Chebyshev's inequality to determine

(a) A lower bound for P(8 < X < 24).

(b) An upper bound for P(|X - 16| ≥ 18).

Q7. Suppose that the distribution of the weight of a prepackaged "1-pound bag" of carrots is N(1.18, 0.07²) and the distribution of the weight of a prepackaged "3-pound bag" of carrots is N(3.22, 0.09²). Now independently select at random three 1-pound bags of carrots with weights being X₁, X₂ and X₃ respectively. Also randomly select one 3-pound bag of carrots with weight being W. Let Y = X₁ + X₂ + X₃.

(a) Find the mgf of Y.

(b) Find the distribution of Y, the total weight of the three 1-pound bags of carrots selected.

(c) Find the probability P(Y < W), i.e., the probability that the sum of weights of three 1-pound bags randomly selected is smaller than the weight of one 3-pound bag randomly selected.

Reference no: EM132312162

Questions Cloud

What you already knew about your bargaining style : What if anything did you learn about yourself? Were you surprised, or did the survey confirm what you already knew about your bargaining style?

Ethical fading in a high-pressure work environment : How might one guard against ethical fading in a high-pressure work environment?

Tremendous enthusiasm and commitment : Krogh has said that he went into his White House job "with tremendous enthusiasm and commitment-almost to a fault."

Develop leadership skills as a critical care paramedic : PMSC20001 - Advanced Clinical Assessment and Decision Making - Central Queensland University - Formulate an appropriate clinical management plan based

Find the inverse transformation : Assignment - Elements of Probability. Consider two random variables X and Y with the joint probability density - Find the inverse transformation

Important to distinguish between fixed and variable costs : Why is it important to distinguish between fixed and variable costs? Calculate the average and incremental cost per case for Kim and Pat.

Develop realistic job preview for flight attendants : You are the HR manager for a commercial airline. You have been assigned to develop a realistic job preview for flight attendants.

Analyse the main factors helping or restricting air cargo : MGT300 LOGISTICS MANAGEMENT T318 KING’S OWN INSTITUTE Australia-Analyse the main factors helping or restricting air cargo development in the United Kingdom.

Multinational firms toward the global environment : What do you think are the responsibilities of multinational firms toward the global environment?

User Account

All Pages