Reference no: EM132371371

Probability Problems - Do the following problems.

1. Consider the minimax criterion for a two-category classification problem.

(a) Fill in the steps of the derivation of Eq. 23:

R(P(ω₁)) = λ₂₂ +( λ₁₂ - λ₂₂)∫_{R_1}p(x| ω₂)dx +P(ω₁)[(λ₁₁ - λ₂₂) + (λ₂₁ - λ₁₁)∫_{R_2}p(x|ω₁)dx - (λ₁₂ - λ₂₂)∫_{R_1}p(x|ω₂)dx].

(b) Explain why overall Bayes risk must be concave down as a function of the prior P(ω₁) as shown in Fig. 2.4.

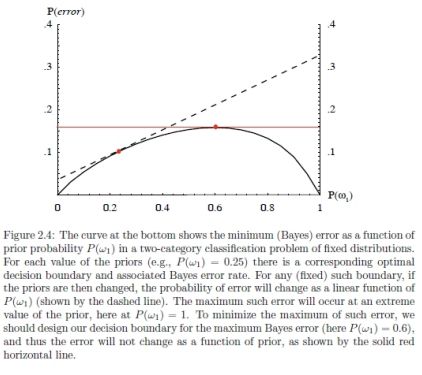
(c) Assume we have one-dimensional Gaussian distributions p(x|ω_i) ∼ N(µ_i, σ_i²), i = 1, 2, but completely unknown prior probabilities. Use the minimax criterion to find the optimal decision point x* in terms of µ_i and σ_i under a zero-one risk.

(d) For the decision point x* you found in (c), what is the overall minimax risk? Express this risk in terms of an error function erf(·).

(e) Assume p(x|ω₁) ∼ N(0, 1) and p(x|ω₂) ∼ N(1/2, 1/4), under a zero-one loss. Find x* and the overall minimax loss.

(f) Assume p(x|ω₁) ∼ N(5, 1) and p(x|ω₂) ∼ N(6, 1). Without performing any explicit calculations, determine x* for the minimax criterion. Explain your reasoning.

2. Let the conditional densities for a two-category one-dimensional problem be given by the Cauchy distribution

p(x|ω_i) = (1/πb)(1/(1+((x-a_i)/b)²), i = 1, 2.

(a) By explicit integration, check that the distributions are indeed normalized.

(b) Assuming P(ω₁)= P(ω₂), show that P(ω₁|x) = P(ω₂|x) if x =(a₁ + a₂)/2, i.e., the minimum error decision boundary is a point midway between the peaks of the two distributions, regardless of b.

(c) Plot P(ω₁|x) for the case a₁ = 3, a₂ = 5 and b = 1.

(d) How do P(ω₁|x) and P(ω₂|x) behave as x → -∞? x → ∞? Explain.

3. (a) Suppose we have two normal distributions with the same covariances but different means: N(µ₁, ∑) and N(µ₂, ∑). In terms of their prior probabilities P(ω₁) and P(ω₂), state the condition that the Bayes decision boundary not pass between the two means.

(b) Consider an example on pp. 45-46 of Lecture 3 with general normal distributions for a 3-class problem. For the given distributions derive the equations of the boundaries between classes (the plots of the boundaries are given in the notes). Compute numerically the coordinates of the two points where the boundaries of all three classes meet.

4. Consider a two-category classification problem in two dimensions with

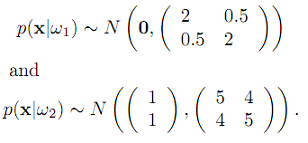
(a) Calculate the Bayes decision boundary.

(b) Calculate the Bhattacharyya error bound.

5. Use the classifier given by Eq. 49:

g_i(x) = -½(x - µ_i)^t _i∑^-1(x - µ_i) - d/2 ln2π - ½ln|∑_i| + lnP(ω_i)

to classify the following 10 samples from the table

in the following way. Assume that the underlying distributions are normal.

(a) Assume that the prior probabilities for the first two categories are equal P(ω₁) = P(ω₂) = ½ and P(ω₃) = 0 and design a dichotomizer for those two categories using only the x₁ feature value.

(b) Determine the empirical training error on your samples, i.e., the percentage of points misclassified.

(c) Use the Bhattacharyya bound to bound the error you will get on novel patterns drawn from the distributions.

(d) Repeat all of the above, but now use two feature values, x₁, and x₂.

(e) Repeat, but use all three feature values.

(f) Discuss your results. In particular, is it ever possible for a finite set of data that the empirical error might be larger for more data dimensions?

Textbook - Duda, Hart, and Stork, Pattern Classification, Wiley, 2-nd edition, 2001.

Attachment:- Probability Problems.rar