Reference no: EM131100425
E15: Fundamentals of Digital Systems - Fall 2015 - HOMEWORK 1
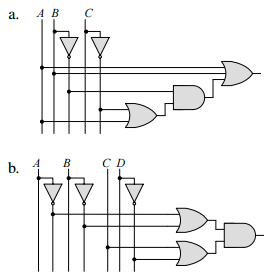
1. Write down boolean expressions for these two logic diagrams.
2. Draw logic diagrams to implement the following Boolean expressions.
a. Y = (A + B')(C' + D)
b. Y = A + B + B'(A + C')
3. Using only the axioms of Boolean Algebra from the handout, prove these two statements. Justify each step using the axioms.
a. x + (x' • y) = x + y
b. x • (x' + y) = x • y
4. A bit vector of length N is defined as a sequence of N boolean values. Denote by BN the set of all possible bit vectors of length N. For example
B2 = {00, 01, 10, 11}
We will define three operations on bit vectors by applying the familiar binary logic operations to their individual elements. In the C programming language, these are known as bitwise operators.
The two binary operators | and & are defined by applying the OR and AND operations on each bit, respectively. For example,
10 | 01 = 01 | 10 = 11
10&01 = 01&10 = 00
The unary operator ~ is defined by taking the bitwise complement of each element of the bit vector. For instance,
~ (11) = 00
For any N ≥ 1, the set BN, together with the three bitwise operators defined above, constitutes a valid Boolean Algebra.
a. Complete the tables below to show the results of the three operations in B2. The examples from above have been filled in to get you started.
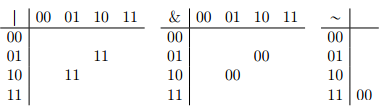
b. What is the identity element of B2 with respect to the | operation? With respect to the & operation? In general, what would each element look like for an arbitrary value of N?
c. Compute the value of the following expression in B8:
10000001 | ~ (00110001 & 10011001)
5. For the function F given by this truth table:
|
x
|
y
|
z
|
F
|
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
0
|
|
0
|
1
|
0
|
0
|
|
0
|
1
|
1
|
1
|
|
1
|
0
|
0
|
1
|
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
0
|
|
1
|
1
|
1
|
0
|
a. Express F as a product of standard sums.
b. Express F as a sum of standard products.
c. Simplify the sum of products to give the expression with the fewest literals. Show your work.
d. Draw a logic diagram for the circuit implementing F based on your simplified expressions.
|
Discuss eighth amendment rights often claimed by prisoners
: Write a 250-350 words and APA format paper that Discuss the Eighth Amendment rights often claimed by prisoners, citing examples.
|
|
Buy the radio with the higher purchase
: Joel is selling a radio cassette with a hire purchase of $360, He can also buy the radio in cash of $300, The deposit is given to be $160. Emmanuel decided to buy the radio with the higher purchase in 4 months how much is his installment?
|
|
Cost analysis to determine the most economical way
: Reconsider the Electronic Toys Co. problem presented in Prob. 10.4-5. Sharon Lowe is concerned that there is a significant chance that the vitally important deadline of 57 days will not be met.
|
|
Would you recommend using private or public warehouses
: Suppose your company sells ice cream, and your competitive strategy involves introducing innovative new flavors to market frequently. Would you recommend using private or public warehouses? Defend your answer.
|
|
Draw logic diagrams to implement boolean expressions
: E15: Fundamentals of Digital Systems - Fall 2015 - HOMEWORK 1. Draw logic diagrams to implement the following Boolean expressions. Y = (A + B')(C' + D) and Y = A + B + B'(A + C')
|
|
What are the next most probable n-strings
: Find the probability of each individual string xn for those values of i.
|
|
Different movie soundtracks in stock
: Jenny White is shopping for CDs. She decides to purchase 3 movie soundtracks. The music store has 10 different movie soundtracks in stock. How many different selections of movie soundtracks are possible?
|
|
The upper path through the project network
: Reconsider the Tinker Construction Co. problem presented in Prob. 10.5-1. While in college, Sean Murphy took an OR course that devoted a month to linear programming, so Sean has decided to use linear programming to analyze this problem
|
|
Question regading the mean value theorem
: Consider the function f(x) = x^2 on the interval [0,1]. According to the Mean Value Theorem, there must be a number c in (0, 1/2 ) such that f ′(c) is equal to a particular value d. What is d?
|