Reference no: EM132356489

Probability Models and Stochastic Processes Assignment -

Q1. Let X and Y be random variables defined on a common probability space. Assuming Var(X) < ∞, show that Var(X) = EVar(X | Y )+ Var(E[X | Y ]). [Hint: Use defn. of Var(X) and conditional expectation tricks.]

Q2. Let X be a non-negative random variable with probability density function (pdf) f.

(a) Show that EX = ₀∫^∞P(X ≥ x)dx.

(b) Using (a), show that E[X^α] = ₀∫^∞αx^α-1P(X ≥ x)dx for any α > 0.

Q3. Let (S_n, n = 0, 1, . . .) be a branching process whose offspring distribution has probability generating function (pgf) G(z). Assume S₀ = 1, and denote by G_n(z) the pgf of S_n, for n = 0, 1, . . . . Show that G_n(z) = G_n-1(G(z)) and that G_n(z) = G(G_n-1(z)) for n = 1, 2, . . . .

Q4. Suppose that each individual of the geobacter stokhastikos bacterial species successfully undergoes binary fission with probability p ∈ (0, 1) and otherwise dies. Assuming that each individual behaves independently and identically, we shall model the number of individuals as a branching process (S_n, n = 0, 1, . . . ).

(a) Write down the pgf, G(z), of the offspring distribution.

(b) Assuming S₀ = 1, determine explicit expressions for the mean and variance of S_n as a function of n. In terms of p, when is μ < 1 (subcritical), μ = 1 (critical), and μ > 1 (supercritical)?

(c) Assuming S₀ = 1, determine the probability of ultimate extinction, η, as a function of p.

(d) Assuming S₀ = 1, determine an explicit expression for G_n(z) = Ez^S_n for n ∈ {1, 2, 3}.

(e) Assuming S₀ = 1, determine η_n = P(S_n = 0) for n ∈ {1, 2, 3}.

(f) Suppose now that S₀ is a random initial population size taking values in N with pgf A(z). Repeat (b)-(e) removing the previous unit initial population size assumption.

Q5. Consider a branching process (S_n, n = 0, 1, . . . ) with S₀ = 1 whose offspring distribution X is a mixture of two types, A and B. Explicitly, X = A with probability p ∈ [0 1] and X = B otherwise. Denote the pgfs of A and B as G_A(z) and G_B(z) respectively.

(a) Denote the "pure" probabilities of ultimate extinction as η_A (i.e. p = 1) and η_B (i.e. p = 0). Write an equation for the general probability of ultimate extinction η in terms of G_A, G_B, and p.

(b) Continuing (a), show that η ∈ [min{η_A, η_B}, max{η_A, η_B}].

(c) Generalize (a) and (b) to determine an equation for the general probability of ultimate extinction, η, for n ∈ {1, 2, 3, . . . } types, denoting the mixing probabilities as p_k and pgfs by G_k(z) for k = 1, . . . , n. Denoting the "pure" probabilities of ultimate extinction as η_k for k = 1, . . . , n, prove that η ∈ [min_kη_k, max_kη_k].

(d) Suppose there are now uncountably infinite types, indexed by some continuous random variable T with pdf f and "pure" probabilities of ultimate extinction η_t known (i.e. probability of ultimate extinction given T = t) with corresponding pgfs G_t(z). Determine an expression for the general (unconditional) probability of extinction η satisfies, and obtain upper- and lower-bounds for η in term of the uncountably infinite sequence of η_t.

Q6. Consider the following process on the infinite two-dimensional square lattice (think of your square graph paper going on forever). Select one vertex to be the origin, and denote it by (0, 0), and label every vertex by (i, j) ∈ Z². On every vertex there is an inflated balloon filled with pins. When a balloon is popped, the pins it releases pops each of its (un-popped) cardinal neighbours with probability p ∈ (0, 1), independent of everything else. Grinning mischievously, you walk up to the origin and pop the balloon there. Denote by B_n the number of balloons which pop a distance of n steps from the origin (in the sense of the Manhattan distance; that is, {(i, j) ∈ Z² for which |i| + |j| = n}).

(a) Write down a model for a branching process (S_n, n = 0, 1, 2, . . .) whose offspring distribution X satisfies P(X ≥ 4) < 1 which is a strict upper bound for B_n; i.e., which you can show satisfies B_n ≤ S_n for all n.

(b) Determine the range of parameter values p for which you can guarantee that the balloon popping process will not go on forever.

Q7. A discrete random variable X is said to have a hypergeometric distribution with positive integer parameters N, n ≤ N, and r ≤ N if it has probability mass function

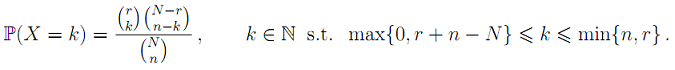
Determine the probability generating function G(z) = Ez^X for |z| ≤ 1. [Hint: You may wish to utilize the so-called hypergeometric function ₂F₁(a, b; c; z), but take care if c is a non-positive number.]

Q8. Let (S_n, n = 0, 1, . . . ) be a branching process with Poisson offspring distribution; that is, with

P(X = k) = e^-λ λ^k/k!, k = 0, 1, 2, . . . ,

where the rate parameter satisfies λ > 0. Determine the probability of ultimate extinction, η, as a function of λ. [Hint: You may wish to make use of the Lambert W function, which satisfies z = W(z)e^W(z) for any z ∈ C.]

Attachment:- Probability Models and Stochastic Processes Assignment File.rar