Calculate the shear resistance provided by the stirrups

Assignment Help Civil Engineering

Reference no: EM133556199

Design for Shear and Flexure

Note: For all problems provide neat drawings and show clearly all calculations. Make any assumptions needed.

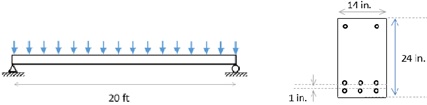
Question 1. The beam shown in the figure has been designed for flexure for a factored uniform load of 10 kips/ft. The concrete strength is 4,500 psi and the steel reinforcement includes is 8 #5 Grade 60 bars as shown in the drawing. In your calculations assume cover of 1 inch is used.

a. Estimate p_b and p_t-c, for positive flexure. Hint: ignore the compression reinforcement.

b. Assess the design for flexure and explain if it is a good or a bad design. If it is not a good design, redesign the beam for flexure.

c. For the design given, calculate the nominal shear strength of the beam section using ACI 318 for Vc, and design the shear reinforcement for three case: i) unreduced shear force and uniform tie spacing, ii) reduced shear force and uniform tie spacing, iii) reduced shear force and nonuniform tie spacing.

2122_Design for Shear and Flexure.jpg

Question 2. A simply supported rectangular beam with a length of span of 32 ft carries its self-weight, an additional dead load of 2.4 kips/ft, and a live load of 1.5 kips/ft. The beam has a width of 12 in., height of 18 in., clear cover for the longitudinal reinforcement of 15 in., and it is constructed with concrete with compressive strength of 3,500 psi and four No. 5 Grade 60 steel bars on the tension side. Considering two loading scenarios, 1.4DL and 1.2 DL+1.6LL,
- Estimate Ρ₀ and Ρ_t-c,: for positive flexure, and assess the flexural design of the beam, as you did in Problem 1. There is no need to redesign this beam.
- Then, design the shear reinforcement in the beam for the: unreduced shear demand, using uniform reinforcement, reduced shear demand, using uniform reinforcement, reduced shear demand and non-uniform spacing. Use the minimum number of stirrups required by specifying two or three areas with different spacing along the half-beam and one area without ties where allowed by ACI.

Question 3. Assume a beam with stirrups inclined at 60° angle with respect to the longitudinal steel resisting cracks developing at 45° angles. Derive analytically the equation that allows you to calculate the shear resistance provided by the stirrups as a function of the stirrup and crack angle.

Reference no: EM133556199

Questions Cloud

Discuss theories that are used in fraud examination : Discuss and describe the following theories that are used in fraud examination: fraud triangle, fraud diamond, fraud pentagon, and Meta Model.

Historical research into Mesopotamia : In the earliest days of historical research into Mesopotamia, the only insight into the minds of the people was their knowledge of the Epic of Gilgamesh.

Describe each standard update : Thoroughly read the last two standard updates. Describe each standard update and what it added to the existing authoritative accounting literature.

Describe your initial thoughts regarding the case : Describe your initial thoughts regarding the case and challenge that you feel you will face with regard to depth and complexity of issues that will be addressed

Calculate the shear resistance provided by the stirrups : Derive analytically the equation that allows you to calculate the shear resistance provided by the stirrups as a function of the stirrup and crack angle

What are three most relevant lessons learned from article : What are the three most relevant lessons learned from the article? What are the three most important best practices of this article?

How would the company accomplish this : If company wanted to take advantage of depreciation expenses, how would this company accomplish this? What would be the advantages? Are there any disadvantages?

What value do businesses using the tbl bring to society : What value do businesses using the TBL bring to society, and how might society be impacted if TBL were not a common business practice?

What is the cost of confronting this spirit : What is the cost of confronting this spirit and what are the virtues that will be required to overcome it?

User Account

All Pages