Reference no: EM131087364

Econ 805 Fall 2009 Problem Set 2-

1. Revenue Comparisons with Risk-Averse Bidders

In our baseline model, we assumed risk-neutral bidders with private values, that is, we assumed ex-post bidder payoffs were

where t_i is bidder i's type and p the payment made by the winner. We showed that with these payoffs and symmetric, independent signals, revenue equivalence holds, so first- and second-price auctions with the same reserve price raise the same expected revenue. In this problem, we introduce risk-aversion by modifying payoffs to

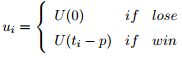
where U is strictly increasing and strictly concave; and we will show that with this change, expected revenue is strictly higher for the first-price auction.

Throughout the problem, we assume N bidders with private values ti which are i.i.d. draws from a probability distribution F.

(a) Show that in a second-price auction with reserve price r, it is still a weakly dominant strategy for risk-averse bidders with type t_i ≥ r to bid their valuations, and for bidders with types t_i < r to bid below r (or not bid).

(b) Normalize U(0) = 0. Suppose the first-price auction with reserve price r has a symmetric equilibrium where bidders with types t_i ≥ r bid b_i = β_U(t_i), with β_U continuous and strictly increasing. Show that β_U(r) = r.

(c) Show that if all his opponents bid according to β_U, a bidder with type t_i > r who bids b earns an expected payoff of

F^N-1 (β_U^-1(b))U(t_i - b)

and therefore that if β_U is a symmetric equilibrium,

(N - 1)f(t_i)/F(t_i)β'_U(t_i) = U'(t_i - β_U (t_i))/U(t_i - β_U (t_i))

(d) If β_RN is the symmetric equilibrium of the first-price auction with risk-neutral bidders, show that β_RN (r) = r and

(N - 1)f(t_i)/F(t_i)β'_RN(t_i) = 1/t_i - β_RN (t_i)

(e) Show that for any function U with U(0) = 0, U' > 0 and U'' < 0 and any x > 0,

U'(x)/U(x) < 1/x

(f) Conclude that

Β'_RN(t_i)/t_i - β_RN(t_i) = (N - 1)f(t_i)/F(t_i) = β'_U(t_i)(U'(t_i - β_U(t_i))/U(t_i - β_U(t_i))) < β'_U(t_i)/t_i - β_U(t_i)

(g) Prove the following ranking lemma, similar to the one we used in class:

Let g : R⁺ → R and h : R⁺ → R are two continuous, differentiable functions. If g(z) ≥ h(z), and for any x ≥ z, g(x) = h(x) → g'(x) > h'(x), then g(y) > h(y) for any y > z.

(h) Use (f) and (g) above (and the fact that β_U(r) = β_RN(r) = r) to show that for all t_i > r, β_U(t_i) > β_RN(t_i).

(i) Now you know that

i. a first-price auction with reserve price r and risk-averse bidders earns greater expected revenue than a first-price auction with reserve price r and risk-neutral bidders;

ii. a first-price auction with reserve price r and risk-neutral bidders is revenue-equivalent to a second-price auction with risk-neutral bidders; and

iii. equilibrium strategies are the same in a second-price auction with reserve price r whether bidders are risk-averse or risk-neutral.

Conclude that when bidders are risk-averse, the first-price auction revenue-dominates the second-price auction.

2. "Buy it Now"

Some online auctions are run as ascending auctions with a "Buy It Now" option, that is, at any point during the auction, any bidder can immediately claim the object at a predetermined price. We will model the ascending portion of the auction as a button auction - the price rises continuously from 0 until either all but one bidder has dropped out or someone has decided to pay the "Buy It Now" price.

Suppose there are two bidders, with independent private values drawn from the uniform distribution on [0, 100]. Suppose the "Buy It Now" price is 50, and that there exists a symmetric equilibrium where both bidders play the following strategy: "If v_i < 50, remain active until the price reaches vi and then drop out. If v_i > 50, remain active until the price reaches g(vi) and then end the auction by bidding the 'Buy It Now' price," where g : [50, 100] → [0, 50] is some function.

(a) Show that if g is strictly decreasing, this auction satisfies the conditions for revenue equivalence.

(b) Show that, conditional on winning, a bidder's expected payment must be the same in this auction as it would be in a standard ascending auction with no "Buy It Now" price or reserve price.

(c) Use this to calculate the function g, that is, the price at which each type of bidder with value above 50 jumps to a bid of 50.

(d) If the seller is risk-averse (but the buyers are risk-neutral), does the seller prefer this auction or a regular ascending auction? What about this auction or a first-price sealedbid auction?

3. Common Values and Information Aggregation

Suppose there is one object for sale via a second-price sealed-bid auction with n bidders. The object is worth V to all bidders, and

The bidders get private signals Xi which are independent, conditional on the realization of V, and take values between 0 and 1. The conditional density of X_i, given V, is given by

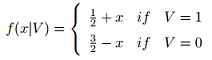
(a) Fix i and let Y₁, . . . , Y_n-1 be the order statistics of X₁, . . . , X_i-1, X_i+1, . . . , X_n. Calculate the joint probability density of (X_i, Y₁) at a point (x, x), conditional on V = 1.

(b) Calculate the joint probability density of (X_i, Y₁) at a point (x, x) conditional on V = 0.

(c) Argue by Bayes' Law that E(V|X_i = Y₁ = x) is .5A/.5A+.5B, where A and B refer to your answers to the first two parts of this question.

(d) Note that everyone bidding b_i(x) = E(V|X_i = Y₁ = x) is an equilibrium. (You don't have to show it.) Show that as n increases, information does not aggregate, that is, the price paid by the winner does not converge in probability to the actual value V. (The easiest way to show this is to show that b_i is bounded above away from 1.)

Now modify the model (as in Pesendorfer and Swinkels) by allowing for more than one object for sale. Suppose that in auction r, there are 2r bidders and r objects for sale using a r + 1^st-price auction (that is, all winners pay the price of the highest losing bid). The objects all have the same (common) value V , and the signal structure is the same as before.

(e) Calculate the joint density of (X_i, Y_r+1) at (x, x) in auction r when V = 1.

(f) Calculate the joint density of (X_i, Y_r+1) at (x, x) when V = 0.

(g) Calculate the equilibrium bid strategy in auction r,

b_i^r(x) = E (V|X_i = Y_r+1 = x)

(h) Show that as r goes to infinity, b_i(x) goes to 1 for x > ½, and 0 for x < ½. Show that this implies that the sequence of auctions {A_r} aggregates information.