Reference no: EM132551538

BME 462 Biomechanics - Kwame Nkrumah University of Science and Technology

Part A
Question 1. a) State the Wolff's law of the transformation of bone.
b) What is the fundamental idea in the trajectorial theory of bone structure?
c) Discuss in detail the composition and structure of bone explaining why the different bone tissues are organized differently.
d) Explain why the bones of the human body are stronger in resisting compression than tension and shear.
e) In the human femur, bone tissue is strongest in resisting compressive force, approximately half as strong in resisting tensile force, and only about one-fifth as strong in resisting shear force. If a tensile force of 8000N is sufficient to produce a fracture, how much compressive force will produce a fracture? How much shear force will produce a fracture?

Question 2. a) What is a viscoelastic material?
b) Discuss in detail the three main characteristics of a viscoelastic material
c) Using the correct combination of the spring and dashpot mechanical models, derive a constitutive equation for the standard linear model.
d) Sketching curves from the derived constitutive equation illustrate how this model is better in representing a viscoelastic material than the Maxwell and Kelvin model.

Question 3. a) Using the method of equilibrium derive the three stress transformation equations
b) Determine the equivalent state of stress on an element at the same point which represents (i) the principal stress, and (ii) the maximum in-plane shear stress and the associated average normal stress. Also, for each case, determine the corresponding orientation of the element with respect to the element shown. Sketch the results on each element.

c) Using Mohr's circle solve the problem in (b) above
d) Draw the 3D Mohr's circles that describe the following state of stress.

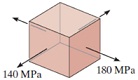
e) From the stress trajectories in the cantilevered beam the solid lines represent the direction of the tensile principal stresses and the dashed lines represent the direction of the compressive principal stresses. The lines intersect the neutral axis at 45 ° angles, and the solid and dashed intersect at 90 °. Why?

Question 4.

a) Explain in detail why no single theory of failure can be applied to a specific material at all times.

b) Give a detailed description, using derivations and diagrams, of one failure theory associated with ductile materials and another with brittle materials.

c) The short concrete cylinder having a diameter of 50 mm is subjected to a torque of 500 Nm and an axial compressive force of 2 kN. Determine if it fails according to the maximum normal-stress theory. The ultimate stress of the concrete is σ_ult = 28 MPa.

d) A material is subjected to plane stress. Express the maximum-shear-stress theory of failure in terms of σ_x, σ_y and τ_xy Assume that the principal stresses are of different algebraic signs.

Part B

Question 5. The forearm and biceps support the 2-kg load at A. If C can be assumed as a pin support, determine the resultant internal loadings acting on the cross Part of the bone of the forearm at E. The biceps pulls on the bone along BD.

Question 6. The 2014-T6 aluminum rod AC is reinforced with the firmly bonded A992 steel tube BC. When no load is applied to the assembly, the gap between end C and the rigid support is 0.5 mm. Determine the support reactions when the axial force of 400 kN is applied.

Esteel = 200GPa , Ealuminum = 73.1GPa

Question 7. If the beam is subjected to an internal moment of M= 30kN.m determine the resultant force caused by the bending stress distribution acting on the top flange A.

Question 8. The solid shaft of radius c is subjected to a torque T at its ends. Show that the maximum

shear strain developed in the shaft is γ_max = Tc/JG. What is the shear strain on an element located at point A, c/2 from the center of the shaft? Sketch the strain distortion of this element.