Question: The weights shown in the figure are in equilibrium. It consists of objects held by vertical strings. The object 3 weighs 1.4 N. The horizontal bars are identical, uniform and each weighs 0.5 N. What is the tension in the upper string?

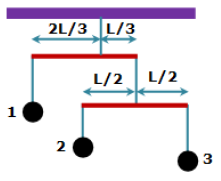
Given that the weight of the object 3, W₃ = 1.4 N The lower rod is in equilibrium. It means the net force and the net torque (i.e., moment of forces) acting on it is zero. The moment of the weights of object 2 and 3 are equal in magnitude

and opposite in direction (counterclockwise for W2 and clockwise for W₃). The weight of this rod (W = 0.5 N) does not produce any torque about the point of suspension as it coincides with the center of gravity of the rod. Hence, from moment equation,

W₂xL/2  - W₃XL/2 = 0 

This gives, W₂ = W₃ = 1.4 N

Tension in the string connecting the upper and lower rods is given by T₁ = W₂ + W + W₃ = 1.4 + 0.5 + 1.4 = 3.3 N (it follows from the fact that net force = 0)

The upper rod is also in equilibrium. It means the net force and the net torque acting on it is also zero. The upper rod is not suspended from its center of gravity. Hence, the weight of this rod (W = 0.5 N) also produces a counterclockwise torque about the point of suspension. The two points are different for this rod. Tension T1 acts downward on this rod and hence produces

clockwise torque on the upper rod.

The distance of the center of gravity from the point of suspension = L/2 - L/3  = L/6

Now, from moment equation

W₁X2L/3 + 0.5XL/6 -T₁XL/3 = 0

W₁ = 1.525 N

Now, the tension in the upper equation

T₂ = W₁ + W + T₁ = 1.525 + 0.5 + 3.3 = 5.325 N (it follows from the fact that net force = 0)