Utilizes augmented matrices to solve out each of the following systems.

x - y = 6

-2x + 2 y = 1

Solution

Now, already we've worked this one out therefore we know that there is no solution to this system. Let's see what the augmented matrix method provides us when we try to use it.

We'll begin with the augmented matrix.

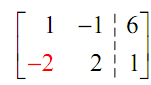
Notice that already we've got a 1 in the upper left corner therefore we don't have to do anything with that.  Thus, we next have to make the -2 into a 0.

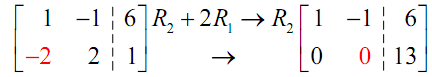
Now, the next step has to be to get a 1 in the lower right corner, however there is no way to do that without varying the zero in the lower left corner. That's a problem, since we must have a zero in that spot plus a one in the lower right corner. What it tells us is that it isn't possible to put this augmented matrix form.

Now, go back to equations & see what we've got in this case.

x - y = 6

0 = 13 ???

The first row only converts back into the first equation. However, the second row converts back to nonsense. We know it isn't true so that means that there is no solution.  Keep in mind, if we attain a point where we contain an equation that just doesn't make sense we have no solution.

Note that if we'd gotten

We would have been okay as the last row would return the equation y = 0 so don't get confused among this case and what we in fact got for this system.

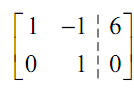
                   Let's sum up what we learned in the previous set of examples. First, if we contain a row wherein all the entries except for very last one are zeroes & the last entry is NOT zero then we can stop & the system will have no solution.

Next, if we obtain a row of all zeroes then we will have infinitely several solutions.  We will then have to do a little more work to get the solution & the number of equations will determine how much work we have to do.

Now, let's see how some systems along with three equations work.  The no solution case will be alike; however, the infinite solution case will have a bit worked to do.