Tests for relative minimum

For a relative minimum point there are two tests:

i.The first derivative, which is

(dy)/(dx)  = f´(x) = 0

ii.The second derivative, which is

(d²y)/( dx²)   = f´(x) > 0

Illustration:

For the function

h(x) = 1/3 x3 + x2 - 35x + 10

Find out the critical values and determine whether these critical values are minima or maxima. Determine the extreme values of the function

Solution

i. Critical values

h(x) = (1/3) x³ + x² - 35x + 10 and

h´(x) = x² + 2x - 35

By using first text,

Then h´(x) = x² + 2x - 35 = 0

Or (x-5) (x+7) = 0

Thus x = 5 or x = -7

ii. The determinant of the minimum and the maximum points needs that we test the value x = 5 and -7 by using the second text

H´´(x) = 2x + 2

a) While x = -7  h´´(x) = -12 <0

b) While x = 5 h´´(x) = 12>0

There x = -7 provides a maximum point and x = 5 provides a minimum point.

iii. Extreme values of the function

h(x) = (1/3) x³ + x² - 35x + 10

While x = -7, h(x) = 189 2/3

While x = 5, h(x) = -98 1/3

The extreme values of the function are h(x) = 189 2/3 that is a relative maximum and h(x) = -98 1/3 , a relative minimum

a) Points of inflexion

The following given are two graphs, points of inflexion can be determined at points P and Q as given below:

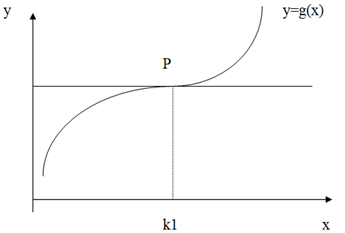
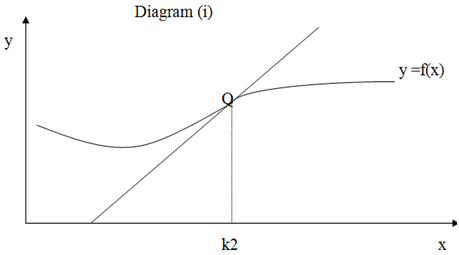
The points of inflexion will occur at point P when

            g´´(x) = 0         at         x = k₁

            g´´(x) < 0         at         x < k₁

            g´´ (x) > 0        at         x > k₁

And at point Q while

           f´´(x) = 0          at         x = k₁

           f´´(x) > 0          at         x < k₁

           f´´(x) < 0          at         x > k₁