System of loads -  Beam:

Build the SFD & BMD for 10 m span simply supported beam subjected to a system of loads as illustrated in Figure .

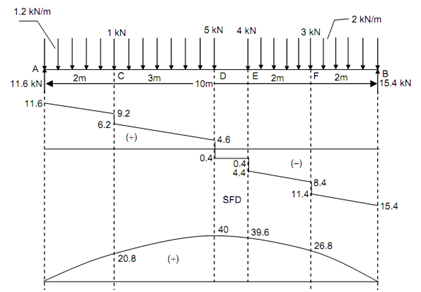
Figure

Taking moment around A and equating to zero.

R _B   × 10 - 2 × 4 × (6 + (4/2)) - 3 × 8 - 4 × 6 - 5 × 5 - 1.2 × 5 × (5/2) - 1 × 2 = 0

R_B = 154 /10 = 15.4 kN

 R_A = (1.2 × 5) + 1 + 5 + 4 + 3 + (2 × 4) - R_B

R_A = 27 - 15.4 = 11.6 kN.

Shear Force (starting from left end) SF at A, F_A = + 11.6 kN

SF just left of C, F_C = + 11.6 - (1.2 × 2) = + 9.2 kN

SF just right of C, F_C = + 9.2 - 1 = + 8.2 kN

SF just left of D, F_D = + 8.2 - (1.2 × 3) = + 4.6 kN

SF just right of D, F_D = + 4.6 - 5 = - 0.4 kN

SF just left of E, F_E = - 0.4 kN

SF just right of E, F_E = - 0.4 - 4 = - 4.4 kN

SF just left of F, F_F = - 4.4 - (2 × 2) = - 8.4 kN

SF just right of F, F_F = - 8.4 - 3 = - 11.4 kN

SF just left of B, F_B = - 11.4 - (2 × 2) = - 15.4 kN

Bending Moment

BM at A and B, MA = MB = 0

BM at F, M =+ (15.4 × 2) - (2 × 2 × (2/2)) =+ 26.8 kN m = + 39.6 kN m

BM at E, M =+ (15.4 × 4) - (3 × 2) - (2 × 4 × (2/2)) =+ 39.6 kN m

BM at D, M =+ (11.6 × 5) - (1 × 3) -(1.2 × 5 × (5/2)  = 40 kN m

                                                                  (considering left side)

BM at C, M =+ (11.6 × 2) - (1.2 × 2 × (2/2)) =+ 20.8 kN m

                                                                    (considering left side)

As the SF changes sign at D, the maximum bending moment occurs at D.

M_max = M_D = + 40 kN m