Submit solutions for all of the following questions. Remember to set out your answers showing all steps completely and explicitly justify your steps.
1. Provide, in no more than two pages, a sample of your working and attempted solutions of various exercise problems that have been set in MAB521/MAN521.
2. Consider an advection diffusion equation describing the evolution of a concentration profile of a dissolved solute in a one-dimensional domain. The advection diffusion model is given by:
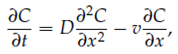
with boundary conditions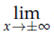
C(x, t) = 0 and initial condition C(x, 0) = f (x).
Here D is the diffusivity and v is the advection velocity.
(a) Show that the advection diffusion equation, including the initial condition and boundary conditions, can be transformed into a linear diffusion equation by introducing new variables x¯ = x - vt and = t.
(b) Using the transformation from part (a) and the fundamental solution developed in class, find and write down the solution for C(x, t) where C(x, 0) _ 0 everywhere except that some mass Q is placed at position x = 0 at t = 0.
(c) For Q = 1 and D = 1, use a computer package to plot
i. C(x, t) at t = 1 for v = 0, v = 0.1 and v = 1.0. Superimpose the three curves on the one axis.
ii. C(x, t) at t = 10 for v = 0, v = 0.1 and v = 1.0. Superimpose the three curves on the one axis.
(d) The method of moments can be used help analyze physical problems that are governed by advection diffusion processes. The first moment of the solution is defined as M1 = ∫x2x1 xC(x, t) dx. Use your solution from part (b) to evaluate the first moment when v = 0 and v 6= 0.
(e) Give a physical explanation for the results you observe in part (d). Describe a practical use for the first moment of the solution?
(f) Without using your solution from part (b), directly evaluate the first moment of the advection diffusion equation for this problem using the governing equation.
State any assumptions that you have made to arrive at your solution.