State the law of radioactive decay. Show that radioactive decay is exponential in nature. Does the activity of a radioactive element depend on external physical conditions?

Law of radioactive Decay: This law states that the number of radioactive nuclei decreases exponentially with time. The rate of disintegration dN/dt, i.e., the number of atoms disintegrated per second is directly proportional to the number of atoms present (N) a that moment. This is known as Decay Law.

Explanation

Let N0 be the number of atoms present in a radioactive sample initially i.e., at t = 0.

Let N be the no of atoms left at a time t and dN be the no of atoms disintegrating in a short interval of time t.

The rate of disintegration = dN/dt

According to decay law = dN/dt α N or dN/dt =  -λN

Where, λ = decay or disintegration constant. The negative sign indicates that as time

increases, the number of atoms decreases

dN/dt=  -λN OR dN/N = -λdt

Integrating the above equation

∫dN/N = -λ∫dt or log_eN = -λt +c ...(1)

Where c = integration constant and it can be found in the initial condition.

i.e., If t = 0, N = N0

Then, logeN0 = c ............ (2)

From equation (1)

LogeN = - λt + logeN0

LogeN - logeN0 = -λt (or)

Loge(N/N₀)= e^{- λt}

Or N= N₀e^{- λt}

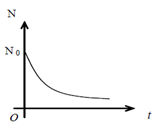
a) The number of radioactive nuclei decreases exponentially with time and reduced to zero after infinite time

b) The above equation represent radioactive decay is exponential in nature. The activity of a radioactivity element does not depend on external physical conditions like temperature, pressure etc.