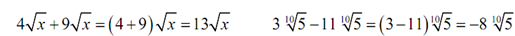Simplify following. Suppose that x, y, & z are positive.

                     √ y⁷

Solution

In this case the exponent (7) is larger than the index (2) and thus the first rule for simplification is violated. To fix this we will utilizes the first & second properties of radicals above. Thus, let's note that we can write the radicand such as

                                                   y⁷  = y⁶ y = ( y³ )²  y

Thus, we've got the radicand written such a perfect square times a term whose exponent is smaller than the index. Then the radical becomes,

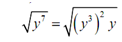
Now employ the second property of radicals to break up the radical and use the first property of radicals then on the first term.

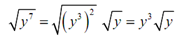
Now this satisfies the rules for simplification and thus we are done.

Before moving to set of examples illustrating the last two simplification rules we have to talk briefly regarding adding/subtracting/multiplying radicals. Performing these operations along with radicals is much alike as performing these operations along with polynomials

Remember again that to add/subtract terms with x in them all we have to do is add/subtract the coefficients of the x.  For instance,

4 x +9 x = ( 4 +9) x = 13x                      3x -11x = (3 -11) x = -8x

Adding/subtracting radicals works in exactly the similar manner.  For example,