Example 2 Solve out following systems of equations.

3x + y - 2z = 2

x - 2 y + z = 3

2x - y - 3z = 3

Solution

Firstly write down the augmented matrix for this system.

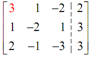
Like with the previous examples we will mark the number(s) which we desire to change in a given step in red. Here the first step is to get a 1 in the upper left hand corner & again, we have several ways to do this. In this we'll notice that if we interchange the first & second row we can obtain a 1 in that spot along with relatively little work.

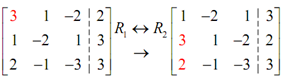
The next step is to get the two numbers below this 1 to be 0's.  Note that this will almost always need the third row operation to do.  Also, we can do both in one step as follows.

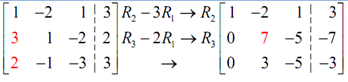
Next we desire to turn the 7 in a 1. We can do it by dividing the second row by 7.

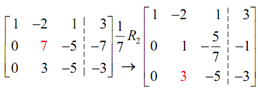
Hence, we got a fraction showing up here. This will happen on occasion therefore don't get all that excited regarding it. The next step is to vary the 3 below this new 1 into a 0.  Note that we aren't going to bother along with the -2 above it quite yet.  Sometimes this is just as easy to turn this into a 0 in the similar step. However in this case, it's possibly just as easy to do it later on as we'll see.

Thus, using the third row operation we get,

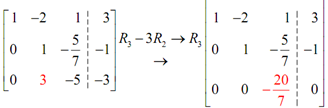
Next, we have to get the number in the bottom right corner into 1.  We can do that  along with the second row operation.

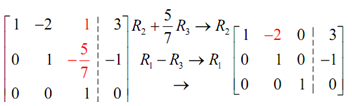
Now, we required zeroes above this new 1.  Hence, by using the third row operation twice as follows will do what we need done.

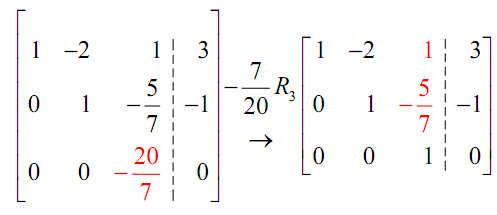
Notice that in this the final column didn't change in this step. That was just because the final entry in that column was zero. Generally, this won't happen.

Then the last step is to make the -2 above the 1 in the second column into a zero. It can easily be done with the third row operation.

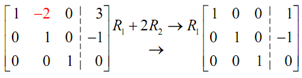
Hence, we have the augmented matrix in the final form and the solution will be,

                           x = 1, y = -1, z = 0

It can be verified by plugging these into all three equations & making sure that they are all satisfied.

                      To solve a system of three equations using Gauss-Jordan elimination can be a lot of work, although it is frequently no more work than directly solving and is several cases less work.  If we were to do a system of four equations (that we aren't going to do) at that point Gauss-Jordan elimination would be less work in all possibility that if we directly solved.

Also, as we illustrated in the final example worked in this section, there actually is no one set path to take through these problems.  Each system is distinct and may need a different path and set of operations to make.  Also, the path that one person determines to be the easiest may not by the path that another person determines to be the easiest.  However, Regardless of the path the final answer will be the same.