Sketch the graph through the process of finding the zeroes

Example Sketch the graph of

                                 P ( x ) = x⁴ - x³ - 6x² .

Solution

Firstly, we'll have to factor this polynomial as much as possible so we can recognize the zeroes & get their multiplicities.

P (x )= x⁴ - x³ - 6x²  = x² + x² - x - 6) = x² ( x - 3) (x + 2)

Following is a list of the zeroes & their multiplicities.

                x= -2( multiplicity 1)

                x= 0( multiplicity 2)

                x= 3( multiplicity 1)

Thus, the zeroes at x= -2 and x= 3 will correspond to x-intercepts which cross the x-axis as their multiplicity is odd & will do hence at an angle as their multiplicity is NOT at least 2. The zero at x= 0 will not cross the x-axis as its multiplicity is even.

The y-intercept is (0, 0) and notice that it is also an x-intercept.

The coefficient of the 4^th degree term is +ve and hence since the degree is even we know that the polynomial will increase without bound at both of the ends of the graph.

At last, following are some function evaluations.

P ( -3) = 54                         P ( -1) =-4         P (1) = -6                P ( 4) = 96

Now, beginning at the left end we know that as we make x more & more -ve the function have to increase without bound.  This means that as we move to the right the graph will in fact be decreasing.

At x = -3 the graph will be decreasing & will continue to decrease while we hit the first x- intercept at x= -2 as we know that this x-intercept will cross the x-axis.

Next, as the next x-intercept is at x=0 we will ought to have a turning point somewhere so that the graph can increase back up to this x-intercept. Again, we won't worry regarding where this turning point in fact is.

Once we hit the x-intercept at x= 0 we know that we've got to have a turning point as this x- intercept doesn't cross the x-axis.  Therefore to the right of x=0 the graph will now be decreasing.

It will continue to decrease till it hits another turning point (at some unknown point) so that the graph can get back up to x-axis for the next x-intercept at x= 3. It is the final x-intercept and as the graph is increasing at this point and have to increase without any bound at this end we are done.

Following is a sketch of the graph.

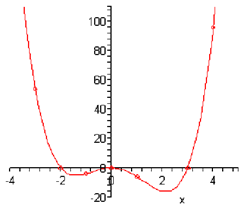
  The procedure that we've utilized in these examples can be a hard process to learn. It takes time to learn how to properly interpret the results.

Also, as pointed out at several spots there are various situations that we won't be capable to deal with here. To determine the majority of the turning points we would require some Calculus, which we obviously don't have.  Also, the procedure does needs that we have all the zeroes and that they all real numbers.

Even with these drawbacks though, the procedure can at least give us an idea of what the graph of polynomial will look like.