Seismic loading principles
Ground motion
Effects of ground motion are specified as one of the acceleration delineation spectrum or time history of acceleration variation methods.
Mapping acceleration should be featured actual ground motion in the construction site during the earthquake as much as possible. For this purpose, at least three Mapping accelerations must be used in the analysis with the following properties.
If the Mapping accelerations are related to the actual earthquake occurred in other areas, it should be tried to that the geology properties, Seismology characteristics, and specially soil layers specifications of accelerometer, be identical with the desired structure place. Intense motion duration at the time of mapping accelerations must be at least equal to 10 seconds or three times more than the main period of the desired structure (whichever is greater)
The selected mapping accelerations must be scaled. In scaling mapping accelerations, ratio effect of the base acceleration, structural significance coefficient, and the inverse of the behavior coefficient (if structure is analyzed with linear elastic method) must be considered. Providing non-linear method analysis, Scaling of mapping accelerations must be done using accepted research methods.
Equaling based on peak ground acceleration for equaling mapping accelerations has been more common than the other methods. To perform this, It is enough to divide the ground acceleration by peak acceleration (A) to obtain the coequal acceleration.
Response spectrum properties
Understanding the response function and Its spectrum is a contribution to understanding the dynamical issues. This spectrum includes important properties some of which is given below :
In fact, response function is the displacement ratio of a system under P0 force in dynamical to static mode. Response spectrum can be divided into three areas: stiff area, stress area, and fine area.
In the stiff area, stimulus frequency is less than the system frequency and In fact The system is so stiff that if we move it by the acceleration (a) from one end, another end also will be moving with the same acceleration (a). In this case, the effect of dynamic behavior is negligible, and dynamic and static displacement are close to each other, and response function is slightly more than one. In stress area, stress occurs due to the closeness of stimulus frequency and natural frequency, and when these two are pretty equal, then:
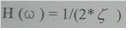
For example, a steel structure with a depreciation factor 0.01 is given by ;

It means that if the system moves a centimeter under a certain force in the static mode, It has 50 centimeters displacements in the stress state. Therefore, stress area prospers such a particular importance and also adjacent points of stress have high response coefficients. By increasing the frequency of the driving force, we get into the soft area where loading is so fast that the system does not sense it. In other words, while the system is starting to react and displacement begins, force direction has changed and the motion inverts and consequently, displacement becomes less than the static mode. This is why structures that have a high period, do not sense the accelerations due to the earthquake which their value is large but their period is low, because loading speed is so fast that structural response settles in soft area.
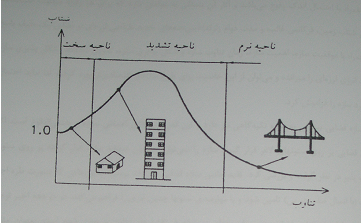
Figure 1-2: Variation of the response acceleration toward the earthquake force
3-2- Structure seismic behavior
Plane spatial trusses form spinal surface and this is the case that the structure is made by steel elements or the aluminium with many connections itself. The combination of this spinal with materials formation and The energy absorption potential of connections, will give very high resistance to the spatial structure against the earthquake. Of course there is some conditions that spatial structure indicates that brittle behavior and fracture of some or even one critical element might be resulted in deterioration of the whole structure. In seismic design, it is required and essential to determine the potential brittle failure modes and providing enough resistance to achieve ductile behavior. Practice using of cylindrical elements in spatial structure is optimum, because they have very appropriate behavior under alternative loading of earthquake.
The seismic load due to ground motion during an earthquake is a function of inertia, stiffness, and attenuation of the structure, and in any case, for design purposes, earthquake force is modeled with a system of external forces. This loading is usually severe and associated with low probability of occurrence and its effects are depended on factors which are different for each earthquake (Such as maximum ground acceleration, prevailing frequency, and duration of the earthquake). New regulations of seismic design have been developed based on a design response spectrum associated with structure location, structure importance, structure frequency, and structure plasticity. Spatial structure plasticity attenuates seismic energy and this property can be used for more economical structural design. But the brittle behavior of the structure shouldn't be forgotten.
Spatial structure behavior is also depended on support structure and this interaction is inevitable and not negligible. If spatial truss settles on thin columns, the structure can't be considered and examined as a spinal surface placed on flexible pillar. Lateral obligation of the spatial structure can be provided by columns which are implemented as contilever (by connecting rigid body to the foundation) or using cluster piles. In the past two decades, spatial trusses behavior has took a lot of worldwide attention, Specially in Japan and china countries. As an example, SAKA has reported the behavior of many spatial structures to the 7.2 magnitude of Kobe(Japan) 1995 earthquake. These buildings include double-layer and single-layer sample in central area of the earthquake. Interesting point in Saka's report is that they have never observed any case of spatial trusses deterioration in this heavy earthquake and this is an emphasis on significance strength and stability of these structures against the earthquake. The only cases that they have mentioned as fracture state is the elements failures which are occured in the vicinity of the fulcrum. The same observations has been reported by Kawagoshi [8].
1-3-2- Snow load effect on period
In usual buildings, snow load has an insignificant effect on dynamic characteristics of the structure such as period and mode form. For example, in an ordinary 6-storey building with the 400 m2 infrastructure surface for each floor, total building mass without snow accounting is almost 2000 tons (considering partitions and walls), while in the most mountainous spots of iran, the load due to the likely heaviest snow will not be exceeded of 80 tons and the presence of such a load, increases period within just 2 percents. In the contrary, in spatial trusses, snow load effects on dynamic chracteristics of the structure due to lightness of structure could be important. In a spatial truss, the unit weight of dead load surface can be decreased about 40 to 50 kg/m2 . Hence, for casing a 400 m2 space, the structure weight itself will be almost 20 tons , while the snow load weight, accounting steep roof reduction, might be reached to 60 tons (400 * 0.150) which is three times more than the weight of the structure itself. Therefore, it can be concluded that snow load has many effects on dynamical characteristics and seismic response of the spatial trusses. Fig. 2-2 shows period variation of some spatial truss drum type models with 20m head and 5m rise toward the snow load. Dead weight of this structure is equal to 50 kg/m2 and it's obvious that when snow load reaches to 150 kg/m2, a significant increase occurs in the period of all samples.
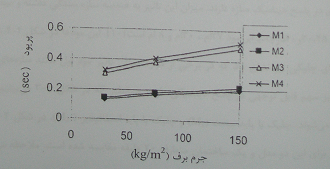
Fig. 2-2: period changes compared with snow mass (Y:period X:snow mass)
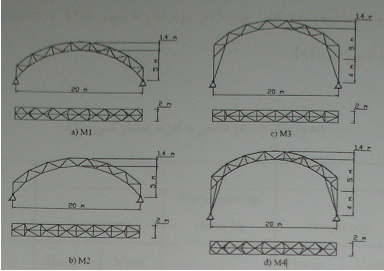
Fig. 3-2: The models considered for structural drum
2-3-2- Effective Mode
In usual trusses, the first mode of the structure often assigns the most vibration energy to itself and contribution of the other modes is so small. Taking a glimpse on Table 1-2 causes to figure out that the first mode weight of buildings up to 10-storey is more than 85% and for second mode is 9%. Then, the contribution level of the first two modes of buildings in structural vibration is 94% in all and another modes portion together is less than 6%. In the contrary, in spatial trusses, higher modes also sometimes have an effective portion in structural dynamic response. Rate of this effect depends on structure geometry and effective mode of the vaults with 45, 30, and 60 degrees casing angle is equal to 37th, 30th, and 8th mode respectively. These modes are shown in Fig. 4-2. Investigating drum trusses also indicates that in some cases, rate of first mode effect is not like usual structures and high modes also have a considerable portion in dynamical response. As shown in Fig. 3-2, these models divided into two groups : drum with a solid foundation (M1) and drum with a flexible foundation (M3). In Fig. 5-2, contribution percentage of horizontal modes has been compared for these two models and a conventional building. It could be noted that in M1 model with a solid foundation, contribution portion for the first mode is 59.7% and the portion of 4th, 6th, and 7th modes is 16.8%, 17.7%, and 6.4%, respectively, while first and second mode's portion of a 20-storey structure has been 80.7% and 10.1% respectively (totally more than 90%) and the portion of the rest of the modes is less than 10% . mode behavior of M3 model with a flexible foundation is similar to conventional structures and horizontal vibrations portion mostly absorbs with 93.5% portion, third mode portion is 4.2% and the portion of other modes is insignificant.
Table 1-2: period and contribution mass
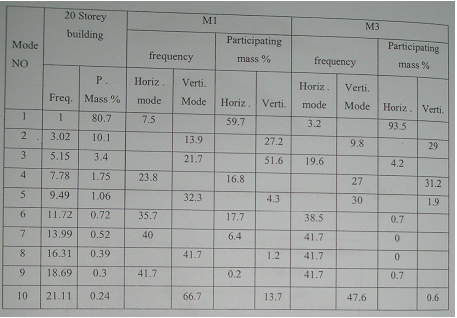
It should be noticed that numbering of these modes is corresponding with the period where the first mode has the highest period and the others place on next classes. By separating horizontal and vertical modes, then it could be said that the portion of the first four modes of the M1 model has been 59.7%, 16.8%, 17.7%, and 6.4%. Then it can be resulted that in arched and cupola structure, as much as structure rise and base flexibility value is fewer, the contribution portion of higher modes will be increased.
3-3-2- Stiffness effect on structure behavior
Increasing stiffness will cause decreasing the period and according to Fig. 1-2, if the structure is in fine area, it takes that to the stress area and increases response acceleration; and vice versa if structure is in stress area, drawn to the fine area and decreases response acceleration. Therefore, increasing stiffness has dual effect on response acceleration and whereas triple areas have no fixed position, it definitely can't be expressed that if structure solidifying causes to increasing or decreasing earthquake forces. It could be resulted by above discussions that the effect of increasing stiffness is sometimes increaser and sometimes reducer, but constantly it has decreasing effect on displacement.