Resultant of coplanar concurrent force system:

The resultant force, of given system of forces can be found out by the resolution method, which is discussed below:

Assume the forces be P₁, P₂, P₃, P₄, and P₅ acting at 'o'. Let OX and OY be the two perpendicular directions. Let the forces subtend angle a₁, a₂, a₃, a₄, and a₅ with Ox respectively. Let R be the resultant and inclined at the angle with OX.

Resolved part of 'R' along OX = Sum of the resolved parts of P₁, P₂, P₃, P₄, P₅ along OX.

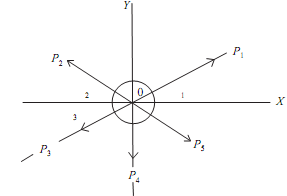
That is

Resolve all the forces horizontally and find algebraic sum of all horizontal components

(which is ∑H)

 

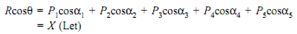
Resolve all the forces in vertical direction and find the algebraic sum of all the vertical components (that is, ∑V)

 

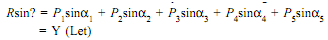
The resultant R of given forces can be given by equation:

   

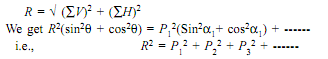
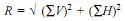
And the resultant force will be inclined at the angle 'θ' with the horizontal, so that

                                                               tanθ = ∑V/∑H