Resolution of Forces by Calculation:

One vector was resolved into two mutually perpendicular components.

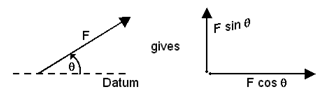
So if there are several vectors each can be resolved into two components.

e.g.    F₁   in directionθ₁,   gives   F₁ sinθ₁,  and  F₁ cosθ₁

          F₂   in directionθ₂,   gives   F₂ sinθ₂,  and  F₂ cosθ₂

          F₃   in directionθ₃,   gives   F₃ sinθ₃,  and  F₃ cosθ₃

          etc.
Once the components have been resolved, they can be added to give a total force in the Datum direction, and a total force perpendicular to the Datum.

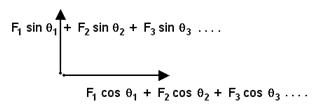
These additions can be done laborio

usly 'by hand' but the modern scientific calculator renders this unnecessary.

Each vector should be entered and multiplied by the cosine of its direction and added consecutively to arrive at a total, F cosθ.

This procedure should be repeated, by multiplying each vector by the sine of its direction, and added consecutively to give F sinθ.

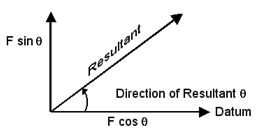
To calculate the Magnitude of the resultant,

          Add  (F sinθ )²  +  (F cosθ)²    (= F²)

And find the square root of the addition  (=F)

To calculate the Direction of the resultant,

          Divide  (F sinθ )  by  (F cosθ)   (= Tanθ)

and find the Angle (direction) that has that resultant,

Note that the values of sine and cosine take both positive and negative values, depending on the direction.

The calculator automatically takes account of this during the procedure.

The only occasion when ambiguity can arise is when finding the angle of the direction (there may be an error of 180º).  This can be resolved by inspection. Note the following:

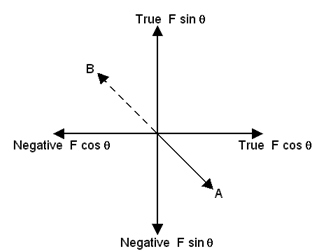
With reference to the ambiguity of direction,

note that 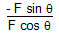 =  (A)  gives the same angle (direction) as   Fsinθ/-FCosθ =  (B).  Thus, F sinθ  and F cosθ  have to be inspected to see which is negative.  Solution (A) or (B) can then be selected.

Similarly,   Fsinθ/FCosθ gives the same result as  -Fsinθ/-FCosθ                    . 

Again, inspect the values of F sin q and F cosθ to see whether both are positive or negative.