Q. What do you understand by the term sparse matrix? How sparse matrix is stored in the memory of a computer? Write down the function to find out the transpose of a sparse matrix using this particular representation.                                                                                                             

Ans.

Sparse Matrix is described below

A m x n matrix A would be a sparse if most of its elements are zero. A matrix that is not sparse is known as dense matrix.

Representing Sparse Matrix in Memory Using Array is described below

In an array representation an array of triplets of type < row, col, element> is used to store non-zero elements, where 1st field of the triplet is used to trace row position second to record column and the 3rd to record the non zero elements of  sparse matrix.

In addition, we are required to record the size of the matrix ( i.e. number of rows and the number of columns) and non zero elements of array of triplets are used for this purpose where the 1st filed saves the number of rows and the 2nd field saves the number of columns and the third field saves the number of non zero elements. The remaining elements of the array saves matrix on row major order. The array representation will be

[2 * (n+1) * size of (int) + n*size of(T)] bytes of memory where n is the number of non-zero elements and T is the data type of the element.

Ex: consider a 5*6 sparse matrix which is written below

Array Representation of Sparse Matrix is given below

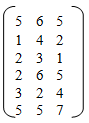
Here n = 5 but the size of array is 6 as first row saves the order of array along with a number non-zero elements.

Memory declaration will be as followsas shown below

# define Max 50 struct triplet

{   int row;

int col;

float element;

}

struct triplet sparse_mat [MAX];

sparse matrix represented as above

[n is the number of non zero elements in array]

for I= 1,2,...n+1 temp = a[I].row a[I].row= a[I].col a[I].col = temp endfor.