Representation in Prolog - Logic Programs:

If we justimpose some additional constraints on first-order logic, so than we get to a representation language knowing as logic programs. There is the main restriction we impose is that all the knowledge we want just to encode is represented as Horn clauses. Hence these are implications that comprise a body and a head is where the predicates in the body are conjoined so they imply the single predicate in the head. Still Horn clauses are universally quantified over whole the variables appearing in them. Then ,there an example Horn clause looks such as:

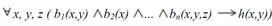
If we notice that the body consists of predicates bi and the head is h(x,y). So there we can make this look a lot much more like the Prolog programs you are needed to writing by making syntactic changes: now first, we turn the implication around and write it as :- like:

∀ x, y, z (h(x,y) :- b (x,y)1 b (x)2 ... b (x,y,z))n

Now finally, we remove the universal quantification it is assumed in Prolog that make the variables capital letters in Prolog requires this to put a full stop at the end:

∀ x, y, z (h(x,y) :- b (x,y), b (x), ..., b (x,y,z))1

Just simplified that we use the notation h/2 to indicate that predicate h has arity 2. In addition we need to call a set of Horn clauses like these a logic program. So for representing knowledge with logic programs is, less expressive than full first order logic,so it can still express lot more of types of information. Obviously in particular, disjunction can be achieved by having alternate or different Horn clauses with the same like head. then, this sentence in first-order logic:

∀x (a(x) b(x) ∨ c(x) d(x))