Rectangular or Cartesian coordinate system

We will begin with the Rectangular or Cartesian coordinate system.  It is just the standard axis system that we employ when sketching our graphs.  Here is the Cartesian coordinate system along a few points plotted.

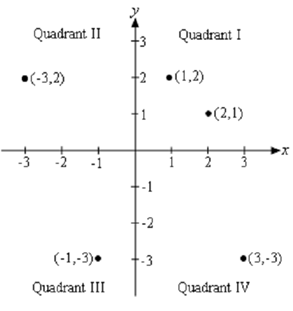
The horizontal & vertical axes, usually called the x-axis & the y-axis respectively, divide the coordinate system up into quadrants as illustrated above.  In each of the quadrant we have the given signs for x and y.

Quadrant I      x > 0 , or x positive     y > 0 , or y positive

Quadrant II     x < 0 , or x negative    y > 0 , or y positive

Quadrant III   x < 0 , or x negative    y < 0 , or y negative

Quadrant IV   x <0 , or x positive      y < 0 , or y negative

Each of point in the coordinate system is described by an ordered pair of the form ( x, y ) .