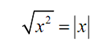Rationalize the denominator for following.  Suppose that x is positive.

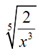
Solution

We'll have to start this one off along with first using the third property of radicals to remove the fraction from underneath the radical as is needed for simplification.

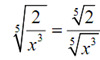
Now, to get rid of the radical in the denominator we required the exponent on the x to be a 5.

It means that we have to multiply by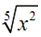 thus let's do that.

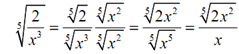
Rationalizing the denominator may appear to have no real uses & to be honest we won't see many uses in an Algebra class.  However, if you are on a track which will take you into a Calculus class you will search that rationalizing is useful on occasion at that level.

Now at last we will discuss general version of the first property of radicals.  Recall that while first we wrote down the properties of radicals we needed that a positive number. It was done to make the work in this section a little simple. Though, with the first property that doesn't essentially have to be the case.

Here is the property for a general a (that means positive or negative)

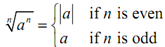
where a  refer to the absolute value of a.  Absolute value always makes a positive number.

Thus, as a rapid example this means that,

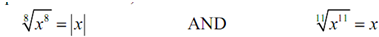
For square roots i.e