Prove the parallelogram law of forces:

Assume that the two forces P and Q act at a point 'O' as shown in figure given below. The force P can be represented in magnitude and direction by vector OA, While force Q is represented in magnitude and direction by vector OB, Angle between the two force is 'a'. The resultant can be denoted by vector OC as shown in the figure given below. Drop perpendicular from C on OA.

Let,

P,Q = Forces whose resultant is needed to be found out.

θ= Angle that the resultant forces makes with one of the forces

α= Angle between the forces P and Q

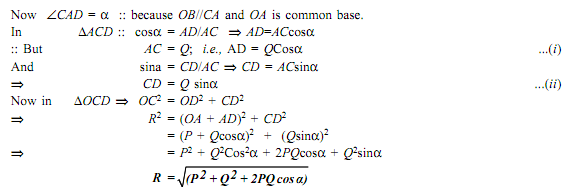
It is the magnitude of resultant 'R'

Direction ( θ ):

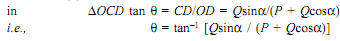
Conditions

(i) Resultant R is max when two forces collinear and are in the same direction.

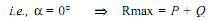
(ii) Resultant R is min when two forces collinear but acting in the opposite direction.

That is  α = 180⁰    =>   R_min = P- Q

(iii) If a = 90⁰, that is when the forces act at right angle, then

R =   P₂  + Q₂

(iv) If the two forces are equal that is, when P = Q  =>R = 2P.cos(θ/2)