HEIGHTS AND DISTANCES

If the angle of elevation of cloud from a point 'h' meters above a lake is α and the angle of depression of its reflection in the lake is  β, prove that the height of the cloud is.

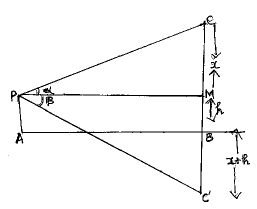
Ans : If the angle of elevation of cloud from a point 'n' meters above a lake is ∝ and the angle of depression of its reflection in the lake is β, prove that the height of the cloud is h

( tan β + tan α / tan β - tan α )

Let AB be the surface of the lake and

Let p be an point of observation such that AP = h meters. Let c be the position of the cloud and c' be its reflection in the lake. Then ∠CPM = ∝ and ∠ MPC1 = β.

Let CM = x.

Then, CB = CM + MB = CM + PA = x + h

In ? CPM, we have tan ∝ = CM /PM

⇒    tan ∝ =  x/AB

[∴ PM = AB]

⇒ AB = x cot∝                        ...........1

In ? PMC', we have

tanβ = C 'M/PM

⇒  tanβ =  x + 2h/AB [Θ C'M=C'B+BM = x + h + n]

⇒  AB = (x + 2h) cot β

From 1 & 2

x cot ∝ = (x + 2h) cot β

x (cot ∝ - cot β) = 2h cot β (on equating the values of AB)

x= (  1/tan α -1/tan β) = 2h /tan β = x(tan β - tan α/tan α - tan β) = 2h /tan β

x = 2h  tan α /tan β - tan α

Hence, the height CB of the cloud is given by CB is given by CB = x + h

⇒ CB= 2h  tan α /tan β - tan α + h

2h tan α    + h tan β - tan α

⇒ CB- 2h tan α + h tan β - h tan α /tan β - tanα= h (tan α + h tan β )/tan β - tan α