The use of arc elasticity in economic analysis involves a good deal of chariness since it is capable of being misinterpreted. Arc elasticity coefficients vary between the same two finite points on a demand curve if direction of change in price is reversed. Arc elasticity for a decrease in price would be different from that for same increase in price between the same to points on a demand curve. For instance, the price elasticity between points J and K - moving from J to K - is equal to 1.11. This is the elasticity for decrease in price from 25$ to 10$. Though a reverse movement on the demand curve, which is from point K to J implies an increase in price from 10$ to 25$ that will give a different elasticity coefficient. In the case of movement from point K to J, P = 10, Δ P = 10 - 25 = - 15, Q = 50 and ΔQ = 50 - 30 = 20. Substituting these values in elasticity formula, we get

E_P = (20/-15)(10/50) = 0.26

Measure of arc elasticity co-efficient in equation I for the reverse movement in price is obviously different from the one given in equation II. So, while measuring the arc elasticity, direction of price change must be carefully noted, otherwise it may yield misleading conclusions.

A method recommended to resolve this problem is to use average of lower and upper values of P and Q in fraction, P/Q, so that formula is

E_p = (δQ/δP). {(P₁+P₂)/2} / {(Q₁+Q₂)/2}

   = (Q₁-Q₂/P₁-P₂). {(P₁+P₂)/2} / {(Q₁+Q₂)/2}

Substituting the values from this illustration, we get

= (30-50/25-10). {(10+25)/2} / {(30+50)/2} = 0.58

This method has its own disadvantages as elasticity co-efficient calculated through this formula, refers to elasticity of demand at mid-point between points J and K (Fig. below). Elasticity co-efficient (0.58) isn't applicable for the whole range of price-quantity combinations at different points between J and K on the demand curve (Fig. below). It gives only mean of the elasticity between the two points. It is vital to note that elasticity between mid-point and the upper point J or lower point K will be different. So this method doesn't give one measure of elasticity.

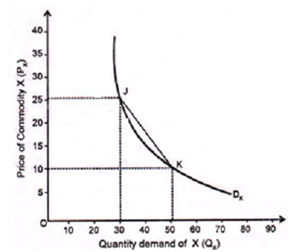
Figure: Measuring Arc Elasticity