Numerical Problems Based on Overhanging Beam:

Q: Draw Shear force diagram for the simply supported beam loaded as shown in the figure given below.

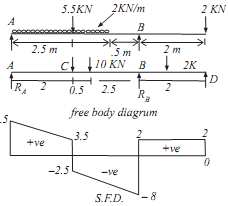
Sol.: Let the reaction at support A and B be, RA and RB First find out support reaction. For finding support reaction, convert UDL in to point load and equal to 2 X 5 = 10KN, acting at the midpoint of UDL that is 2.5m from point A.

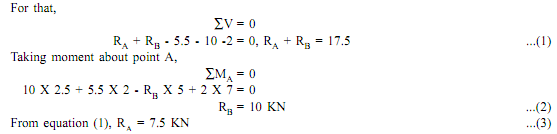
Calculation for Shear force Diagram

Draw section line, here total 3-section line, which break the load RA, 5.5KN (Between A and E),

5.5KN and UDL (Between E and B),

Point B and 2KN (Between B and C). Let

Distance of section 1-1 from A is X₁

Distance of section 2-2 from A is X₂

Distance of section 3-3 from A is X₃

Take left portion of the beam

Take section 1-1

The force on left of section 1-1 is R_A and UDL (from the joint A to the section line which is UDL on total distance of X₁

SF_1-1  = 7.5 -2X1  KN (Equation of the straight line)

It is Equation of straight line (Y = mX + C), inclined linear.

Inclined linear means that the value of shear force at both the nearest point of section varies with X₁  = 0 to X₁  = 2

That is inclined line -2 to -8

As shear force changes the sign so at any point shear force will be zero and at that point bending moment is highest.

For finding position of zero shear force equate shear force equation to zero, that is,

2 - 2X₂; X₂  = 1m, that is at 1m from point A bending moment is maximum.
Take section 3-3

SF_3-3  = 7.5 - 5.5 -10 +10 = 2KN (constant value)

Constant value means that the value of shear force at both nearest point of the section is equal that is

SF_B = SF_C  = 2KN                                                                                                                        ...(7)

Plot the SFD with the help of obtained shear force values.