NUMBER SYSTEM:

 We are familiar with decimal number system which uses ten distinct symbols from 0...9, and has base 10. In the decimal number system a number n₄n₃n₂n₁ is interpreted as 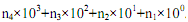. Thus decimal number 5632 represents 5000+600+30+2. It is a weighted code system since numbers 5632, 2563, 3562, 6532 all represent different quantities despite the fact that all of them use the same symbols (2,3,5,6). The magnitude/ value of a number is determined both by the symbols used and the places at which they are present. Thus, symbol 3 at ten's place represent 30, but when written at thousands' place it represent 3000. Although we use only the decimal number system in everyday applications but there are many other number systems possible. In fact, we can have number system with any base r.

  A number system with base r will have r distinct symbols, from 0 to r-1. Binary number system (r = 2), octal number system (r = 8) and hexadecimal number system (r = 16) are some of the frequently used number systems in computer science. Binary number system has two distinct symbols 0 & 1; Octal has seven distinct symbols 0,1,2,3,4,5,6,7; and Hexadecimal number system has sixteen distinct  symbols namely 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. The numbers written in a particular number system can be transformed to an equivalent value in a different number system.

For example a number 3F in hexadecimal is equivalent to 63 (3×16¹ + F × 16⁰) in decimal number system. And similarly a number 302 in octal is equivalent to 194 (3× 8² + 0 × 8¹+2 × 8⁰) in decimal number system.