We can also indicate a strict mathematical/formula definition for absolute value.  It is,

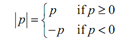
It tells us to look at the sign of p & if it's positive we just drop the absolute value bar. If p is -ve we drop the absolute value bars & then put in a -ve in front of it.

Thus, let's see a couple of quick instance.

|4| = 4                            because 4 ≥ 0

|-8 |  = -(-8) = 8              because - 8 < 0

|0| = 0                             because 0 ≥ 0

Note that these give accurately the same value as if we'd utilized the geometric interpretation.

One way to think of absolute value is that this takes a number & makes it +ve.  Actually we can guarantee that,

                                                               |p |≥ 0

regardless of the value of p.

However we do have to be careful to not misuse either of these definitions. For instance we can't employ the definition on

                                                                      |- x|

since we don't know the value of x.

Also, don't commit the mistake of supposing that absolute value only makes all minus signs into plus signs.  In other terms, don't make the following mistake,

                                                    |4x - 3| ≠ 4x + 3

If you aren't certain that you believe that plug in a number for x. For instance if x = -1 we would get,

                                7 = |-7| =| 4 ( -1) - 3 ≠ 4 ( -1) + 3 = -1

There are a several problems with this.  First, the numbers are apparently not the same and so that's all we actually have to prove that the two expressions aren't the similar.  However there is also the fact that the right number is negative & we will never acquire a negative value out of an absolute value! That also will guarantee that these two expressions aren't the similar.

The definitions above are simple to apply if all we've got are numbers within the absolute value bars. Though, once we put variables within them we've got to begin being very careful.

Now it's time to begin thinking about how to solve equations which contain absolute values.  Let's begin fairly simple and look at the following equation.

                                                          |p| = 4

Now, if we think about this from a geometric viewpoint this means that whatever p is it have to have a distance of 4 from the origin.  Well there are just two numbers that have a distance of 4 from the origin that is 4 and -4.  Thus, there are two solutions to this equation,

                                                      p = -4        or p = 4

Now, if you think regarding it we can do this for any +ve number, not just 4.  Thus, this leads to the following general formula for equations including absolute value.

If         |p| = b, b = 0    then        p = -b     or p = b

Notice that this does need the b be a +ve number.  We will deal along with what happens if b is zero or negative in a bit.