Making Equally Sized Groups : By the time children reach Class 1 or 2, they would have had many experiences of pairs of objects-pairs of shoes, pairs of eyes, ears, arms, legs, wings, etc. They would also have seen groups of three, like the legs of a tripod, the leaves of 'flame of the forest' (see Fig. l(a)), blades of a fan, etc. Or, if we think in terms of groups of four, they may be familiar with the petals of the mustard flower legs of a table/chair/dog. Wheels of a car, etc For introducing them to the idea of gathering groups of a given size, you could ask them to consider objects which form such natural groups of small numbers.
They could also be asked to collect seeds, straws, beads, marbles, etc., and each child (or group of children) could make equal-sized sets of her choice (or the group's choice).
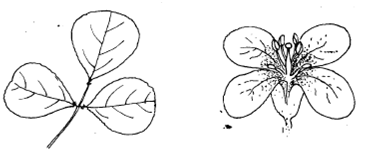
(a) (b)
Figure:(a) A set of leaves of 'flame of the forest', b) a mustered flower.
Another activity that could be thought of for this is telling 'number tales'. You could create an imaginary story in which groups of two (or three, or four, etc.) appear. For instance, you could say, "Now I shall tell you a story of 'two'. You have to tell me how many sets of two are in the story. Raju and his sister were going home from school. On the way they saw a parrot lying on the ground. It was hurt. It tried to move its wings, but could not. Just then, a man came there riding a bicycle with red tyres. He had a pair of blackbirds in a cage. He saw the parrot, picked it up with both his arms, and put it in the cage." You could do similar activities using pictures that have many things (birds, animals, etc.) in groups of different sizes. The children could be asked to identify the groups of 2 objects in it, then those of 3 objects, and so on.
Here is a related exercise for you.
El) Create stories of '5' which may help children identify groups of 5.
Multiplication begins when children add groups of equal size. Let us see how we can help children pick up this ability, and master it.