Load shared by concentric springs:

Two concentric springs are subjected to an axial load of 60 kN. The maximum permissible deflection of the springs is 45 mm & the solid length is 55 mm. If the springs are of the material having G = 80 × 10³ N/mm² and the maximum permissible shear stress is 800 N/mm², determine

a. load shared by the springs, and

b. wire diameter and outer spring radius.

Take inner spring radius = 40 mm & radial clearance = 3 mm.

Solution

The springs are in parallel. Deflection of both of the springs is similar.

Δ= 64 W R³ n / G d ⁴

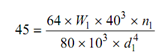
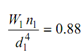          ----------- (1)

τ_max      = 16 W R  /π d³

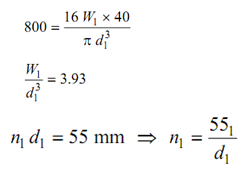------- (2)

  n₁d₁= 55mm   ⇒  n 1 = 55₁ /d₁                           --------- (3)

From Eq. (1) and (3), we get

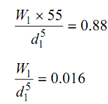--------- (4)

From Eq. (2) to Eq. (1), we get

∴          d₁  = 15.67 mm ; 15.7 mm

∴ W₁  = 3.93 × 15.73  = 15 129 N = 15.1 kN

  W₁  + W₂  = 60 kN

  W₂  = 44.9 kN

Outer Spring

R₂ = 80 + 15.7 + 2 × 3 + d₂ /2= (50.85 + 0.5 d₂) mm

τ max  =16 W R  / π d³

16 × 44.9 × 103 × (50.85 + 0.5 d 2 )

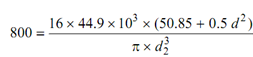
∴          d₂  = 24.4 mm

∴ R₂  = (50.85 + 0.5 × 24.2) = 63.05 mm