The first particular case of first order differential equations which we will seem is the linear first order differential equation. In this section, unlike many of the first order cases which we will watch, we can in fact derive a formula for the general solution. Below, the general solution is derived.

Though, I would suggest you that you do not learn the formula itself. In place of memorizing the formula you must memorize and know the process which I'm going to utilize to derive the formula. Most problems are in fact easier to work by utilizing the process in place of using the formula.

Thus, let's see how to resolve a linear first order differential equation. Keep in mind as we suffer this process that the goal is to reach a solution which is in the form y = y (t).  It's mostly easy to lose sight of the object as we use this process for the first time.

So as to solve a linear first order differential equation we MUST begin along with the differential equation in the form demonstrated below. If the differential equation is not in such form so the process we're going to utilize will not work.

dy/dt = p (t) y + g (t)                    .....(1)

Here both p (t) and g (t) are continuous functions.  Recall that a dirty and rapid definition of a continuous function is as a function will be continuous given, you can draw the graph starting left to right without ever picking up your pen or pencil.  Conversely, a function is continuous if there are no breaks or holes in it.

Here, we are going to suppose that there is some magical function somewhere out there in the world, µ (t), termed as an integrating factor. Do not, at this point, worry regarding what this function is or where this came from. We will figure out what µ (t) is once again we have the formula for the general solution we determine.

Hence, now that we have assumed the existence of µ   (t) multiply everything in equation (1) by µ (t). It will provide:

µ (t) (dy/dt) + µ(t) p (t) y = µ(t)g(t)     .....................(2)

Then, it is where the magic of µ (t) comes in play. We are going to suppose that whatever µ (t) is, it will satisfy the subsequent.

µ(t) p (t) = µ'(t)    .............................(3)

Again do not worry regarding how we can get a µ(t) which will satisfy (3). As we will notice, provided p(t) is continuous we can determine it. Thus substituting (3) in (2) we now reach.

µ (t) (dy/dt) + µ'(t) y = µ(t)g(t)     .....................(4)

At such point we require recognizing that the left side of (4) is nothing more than the subsequent product rule.

µ (t) (dy/dt) + µ'(t) y = (µ(t)y(t))'

Consequently we can replace the left side of (4) along with this product rule. By doing this (4) turns into:

(µ (t) + y(t))' = µ(t)g(t)     .....................(5)

Here, recall y(t) then we can now do something regarding that.  All we require to do is integrating both sides then utilize a little algebra and we will have the solution. Thus, integrate both sides of (5) to find.

∫((µ (t) + y(t))') dt = ∫(µ(t)g(t)) dt

  µ (t) y(t) + c = ∫(µ (t) g(t)) dt   ......................(6)

Remember that the constant of integration, c, starting the left side integration is comprised now. This is vitally significant that this be comprised. If this is left out you will find the wrong answer every time.

The last step is then several algebra to resolve for the solution, y(t).

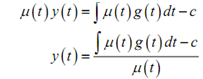
This time, from a notational standpoint we identify that the constant of integration, c, is an unidentified constant and thus to make our life easier we will absorb the minus sign opposite it in the constant and use a plus in its place. It will NOT influence the last answer for the solution. Thus with this change we contain.

y(t) = ∫(( µ (t) y(t))dt + c) / µ (t)   ..............................(7)

Once more, by changing the sign on the constant will not influence our answer. If you decide to remain the minus sign you will determine the similar value of c as I do except this will have the reverse sign.  On plugging in c we will determine exactly the similar answer.

There is various playing fast and loose along with constants of integration in this region, so you will require to get used to this. As we do this we will all the time to try to make this very clear what is going on and try to justify or validate why we did what we did.

Thus, now that we've found a general solution to (1) we require going back and determining just what this magical function µ (t) is. It is really an easier process than you might think.  We'll begin with (3).

µ(t) p(t) = µ′(t)

Divide both sides via µ (t),

p(t) = µ′(t)/ µ(t)

Currently, hopefully you will know the left side of this.

(In µ(t))' = p(t)

As along with the process above all we require to do is integrate both sides to determine.

In µ(t) + k = ∫p(t) dt

In µ(t) = ∫p(t)dt + k

You will see that the constant of integration from the left side, k, had been shifted to the right side and had the minus sign absorbed in it again as we did previous. Also remember that we are using k now as we've previously used c and in a little bit we will have both of them in similar equation. Thus, to ignore confusion we used various letters to represent the fact that they will, in all chance, have various values.

Exponentiate both sides to find µ(t) out of the natural logarithm.

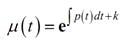
Here, it's time to play quick and loose along with constants again. This is inconvenient to contain the k in the exponent consequently we're going to find it out of the exponent in the subsequent way.

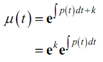
Recall x^a+b = x^a x^b !

Now, let's make use of the fact that k is an unidentified constant. If k is an unidentified constant then consequently is e^k so we might as well just rename this k and create our life easier. This will provide us the subsequent.

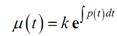
  ...........(8)

Thus, we now contain a formula for the general solution equation (7) and a formula for the integrating factor, equation (8). We do have a difficulty though.  We've got two unidentified constants and the more unidentified constants we have the more difficulty we'll have later on. So, this would be nice if we could determine a way to remove one of them but we'll not be capable to remove both.

It is in fact quite easy to do.  Initially, substitute (8) in (7) and rearrange the constants.

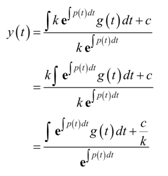
Thus, (7) can be written in as a manner that the only place the two unknown constants demonstrate up is a ratio of the two. After that as both c and k are unidentified constants thus is the ratio of the two constants. Thus we'll just call the ratio c and after that drop k out of (8) as it will just get absorbed in c finally.

The solution to a linear first order differential equation is after that:

y(t) = ∫(( µ (t) g(t))dt + c) / µ (t)   ......(9)

Here,

µ (t) = e^{∫p(t) dt}   ............................(10)

Here, the actuality is that (9) is not as helpful as it may appear.  This is frequently easier to just run during the process that determined us to (9) quite than using the formula. We will not utilize this formula in any of my illustrations. We will require using (10) regularly, as that formula is simple to use than the process to derive this.