Learning Decision Trees Using ID3

Specifying the Problem

We now have to look at how you mentally created your decision tree when deciding what to do at the weekend. One way would be to use some background information as axioms and assume what to do. For example, you could know that your parents actually like going to the cinema, and that your parents are in town, so therefore (using something  like Modus Ponens)  you would choose to go to the cinema.

Other way in which you could have made up your mind was by generalizing from last experiences. suppose  that you remembered all the times when you had a really great weekend. A few weeks before, it was sunny and your parents were not tripping, you played tennis and it was good.  Before a month, it was raining outside and you were  cleaned out,  but  a  trip  to  the  cinema  cheered  you  up.  And  so on.  This information must have guided your decision making, and if that was the case, you might have used an inductive, rather than deductive, procedure to create your

decision tree. actually, it's like human reasons to solve decisions using both inductive and deductive methods. We may state the problem of  learning decision trees as given below:

We have a group of examples exactly categorized into categories (decisions). We also have a set of features defining the examples, and every feature has a fixed set of data which it may possibly have. We need to use the examples to learn the arrangement of a decision tree which may be used to choose the category of an unseen example.

supposing that there are no inconsistencies in the data (when two examples have just similar values for the features, but are categorized dissimilarly), it  is obvious that we may always make a decision tree to exactly decide for the training cases with 100% correctness. All we need to do is make sure each condition is catered for down some branch of the decision tree. Definitely, 100% accuracy may point to over fitting.

The basic idea

In the decision tree given on top, it is major that the "parents visiting" node came at the top of the tree. We don't know accurately the reason for this, as we didn't see the example weekends from which the tree was constructed. However, it is likely that the number of weekends the parents tripped was relatively more, and each weekend they visited, there was a trip to the cinema. Assume, for example, the parents have tripped each fortnight for a year, and on every event the  family went to cinema. This means that there is no proof in favor of doing anything other than watching a movie when the parents come. Given that we are learning laws from examples, this means that if the parents come, the decision is already done. Hence we may keep this at the top of the decision tree, and disregard all the examples where the parents tripped when creating the rest of the tree. Need not to worry about a group of examples will do the construction job more easy.

This sort  of thinking  underlies the ID3 algorithm for  learning  decisions trees, which we will define more formally below. However, the reasoning is a little more delicate, as (in our example) it would also take into account the examples when the parents did not visit.

Entropy

Keeping together a decision tree is all a matter of deciding which feature to check at every node in the tree. We shall describe a measure known as information gain which will be used to choose which feature to check at every node. Information gain is itself deliberate using a measure known as entropy, which we first define for the case of a binary decision problem and then define for the common case.

Given a binary categorization, C, and a group of examples, S, for which the proportion of examples categorized as positive by C is p+  and the proportion of examples categorized as negative by C is p-, then the entropy of S is:

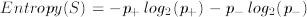
The reason we described entropy first for a binary decision problem is because it is more easy to have an impression of what it is trying to measure. Tom Mitchell keeps this quite good:

"In order to describe information gain shortly, we start by describing a measure generally used in information theory, known as entropy that characterizes the impurity of an arbitrary group of examples."

Suppose having a group of boxes with some balls in. If all the balls were in a single box, then this should be well ordered, and it would be very easy to search a particular ball. If, however, the balls were distributed amongst the boxes, this would not be well ordered, and it should have quite a while to search a particular ball. If we were going to describe a measure based on this notion of purity, we would need to be able to calculate a value for every box based on the number of balls in that, then have the sum of these as the complete measure.  We would  need  to  reward two conditions: closely blank boxes (very clear), and boxes with closely all the balls in (also very clear). This is the basis for the common entropy measure, which is described as follows:

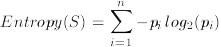
Given an random categorization, C into categories c1, ..., cn, and a set of examples, S, for which the amount of examples in ci is pi, then the entropy of S is:

This measure assures our criteria, because of the -p*log2(p) production: when p gets near to zero (i.e., the category has just  a few examples in it), then the log(p) becomes a wide negative number, but the p part leads the calculation, so the entropy works out to  be closely zero.  Remembering that  entropy calculates the confusion in the data sequence, this low score is good, as it reflects our wish to reward

categories with some examples in. And the same, if p gets near to 1 (i.e., the category has major of the examples in), then the log(p) part gets very near to zero, and it is this which dominates the calculation, so the overall value gets close to zero. Hence we notice that both when the category is closely or completely blank, or when the category closely includes or completely contains  all the examples, the score for the category would be close to zero, which models what we needed it to. Notice that 0*ln(0) is taken to be zero by convention.