Integration

Integration is the reversal of differentiation An integral can either be indefinite while it has no numerical value or may definite while have specific numerical values Integration is represented by the sign ?f(x)dx.

Rules of integration

i.The integral of a constant

?adx = ax +c;    whereas; a = constant

Illustration

Find the following

a)  ?23dx

b)  ??2dx  ; whereas ? is a variable independent of x, hence it is treated as a constant.

Solution

i.  ?23dx = 23x + c

ii. ??2dx. = ?2 x + c

ii.  The integral of x raised to the power n

?xⁿ dx = 1/((n+1). xⁿ⁺¹+ c

Illustration

Find the following integrals

a) ?x²dx

b) ?x^-5/2 dx

Solution

i. ?x²dx = (1/3)x³ + c

ii.  ?x^-5/2 dx = -(2/3)x^3/2 + c

iii). Integral of a constant times a function

? af(x) dx = a ? f(x) dx

Illustration

Determine the given integrals:

i.?ax³dx

ii.?20x⁵dx

Solution

a). ?ax³dx = a ? x³ dx

= (a/4) x⁴ + c

b). ?20x⁵dx = 20 ?20x⁵dx

= (10/3) x⁶ +c

iv). Integral of sum of two or more functions

?{f(x) + g(x)} dx = ?f(x)dx + ?g(x) dx

?{f(x) + g(x) + h(x)}dx = ?f(x)dx + ?g(x)dx + ?h(x)dx

Illustration

Find the given

i.          ?(4x² + ½ x^-3) dx

ii.         ?(x^3/4  + 3/7 x^{- ½} + x⁵)

Solution

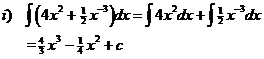
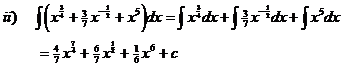
v. Integral of a difference

?{f(x) - g(x)} dx = ?f(x)dx - ?g(x) dx