Indeterminate form : The 0/0 we initially got is called an indeterminate form. It means that we don't actually know what it will be till we do some more work.  In the denominator typically zero means it's undefined. Though that will only be true if the numerator isn't also zero.  Also, in the numerator zero usually means that the fraction is zero, unless the denominator is also zero. Similarly anything divided by itself is 1, unless we're talking regarding zero.

Hence, there are actually three competing "rules" here & it's not clear which one will win out.  It's also a chance that none of them will win out & we will get something completely different from undefined, zero, or one. For instance, we might get a value of 4 out of this, to pick a number totally at random.

There are several more kinds of indeterminate forms

Let's check couple of more examples.

Example   Evaluate the given limit.

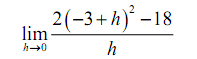
Solution

In this case we also obtain 0/0 and factoring is not actually an option.  Though, till there is some simplification that we can do.

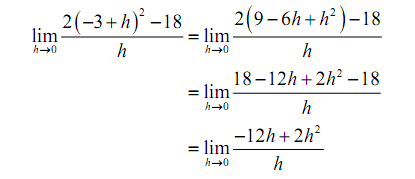
Hence, upon multiplying out the first term we get a little cancellation and notice that we can factor out an h out of both terms in the numerator that will cancel against the h in the denominator and the division by zero problem goes away & then we can evaluate the limit.

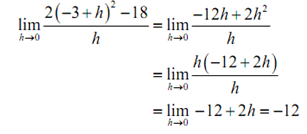
Let's take a look at another type of problem which can arise in computing some limits including piecewise functions.