Important point about the De casteljeau algorithm

1)     

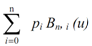
Bezier Curve: P (u) =

   ................     (1)

Here B_n,i (u) = ⁿc_i uⁱ (1 - u) ^n-i       ..............        (2)

C (n, i) = nC_i = n!/i!(n - i)!      0 ≤ u ≤ 1

2)      Cubic Bezier curve has n = 3 as:

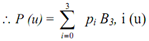
------------------(3)

= p₀ B_{3, 0} (u) + p₁ B_{3, 1} (u) + p₂ B_{3, 2} (u) + p₃ B_{3, 3} (u)

Now, let's find B₃, 0 (u), B₃, ₁ (u), B_{3, 2} (u) , B_{3, 3} (u) by using equation as in above:

Bn, i (u) = nci u (1 - u)

a)  B3, 0(u) = 3C0   u0   (1 - u)3 - 0

=          3!       . 1. (1 - u)3 = (1 - u)3

       0!(3 - 0)!

b)  B3, 1(u) = 3C1   u1   (1 - u)3 - 1

=          3!       . u. (1 - u)2 = 3u (1 - u)2

1!(3 - 1)!

c) B3,2(u) = 3C2   u2   (1 - u)3 - 2

=          3!       . u². (1 - u) = 3u²(1 - u)

       2!(3 -2)!

B3,3(u) = 3C3   u3   (1 - u)3 - 3

=          3!       . u³. (1 - u) 

         3!(3 -3)!

By using (a), (b) , (c) and (d) in (5) we find here:

P (u) = p₀ (1 - u)³ + 3p₁u (1 - u)² 3p₂u² (1 - u) + p₃ u³