Horizontal Curves - Railways

In railway engineering, the horizontal curve is defined by its degree as well as by its radius. The degree is the angle subtended at the centre by a chord of 100 ft (30.5 m).

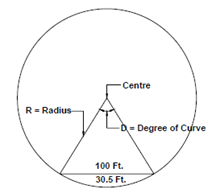
Figure: Degree of a Curve

D = 360/2π R× 30.5

assuming that the length of chord and arc is the same.

= 1750/R

For Broad Gauge, the maximum degree of curvature permitted is 10⁰ or 175 m radius.

When a train is travelling on a curve, the outer rail has to be raised with respect to the inner rail to counteract the centrifugal force (Figure).

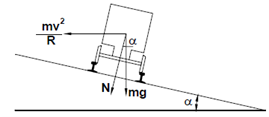
Figure: Force on a Vehicle Moving on a Curved Path

The super-elevation (or cant) is given by the equation:

e =       V²/gR

where  e =  Superelevation,

v =  Speed in m/sec,

R = Radius in m, and

g = Acceleration due to gravity.

= V²/127 R

where  V =  Speed in Km/hr.

The maximum super-elevation provided on a BG track is 165 mm. A horizontal curve requires transitional ends.