Now we need to discuss graphing an equation. The first question which we have to ask is what accurately is a graph of an equation?  A graph is the set of all the ordered pairs whose coordinates satisfy the equation.

For example, the point( 2, -3) is a point on the graph of y = ( x -1)²  - 4 whereas (1, 5) isn't on the graph. How do we tell this?  All we ought to do is take the coordinates of the point and plug them into the equation to see if they satisfy the equation.  Let's do that for both to check the claims made above.

(2, -3) :

In this case we have x= 2 and y = -2 thus plugging in gives,

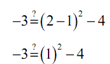
                                               -3 = -3              OK

Thus, the coordinates of this point satisfies the equation and therefore it is a point on the graph.

(1, 5) :

Here we have x = 1 and y = 5 .  Plugging these in gives,

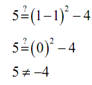                                              NOT OK

The coordinates of this point do not satisfy the equation & so this point isn't on the graph.

Now, how do we sketch the graph of an equation? Certainly, the answer to this based on just how much you know regarding the equation to start off with.  For example, if you know that the equation is a line or a circle we've got easy ways to find out the graph in these cases. There are also several other kinds of equations that usually we can get the graph from the equation without a lot of work.  We will see several of these in the next chapter.

Though, let's assume that we don't know ahead of time just what the equation is or any of the ways to rapidly sketch the graph.  In these cases we will have to recall that the graph is simply all the points which satisfy the equation.  Thus, all we can do is plot points.  We will pick values of x, calculate y from the equation & then plot the ordered pair given by these two values.

How, do we find out which values of x to select? Unluckily, the answer there is we guess. We pick some values & see what we get for a graph. If it looks as we've got a nice good sketch we stop.  If not we pick some more.  Knowing the values of x to choose is really something which we can just get with experience & some knowledge of what the graph of the equation will maybe look like.  Optimistically, you will have acquired some of this knowledge.