Example1:  Solve the subsequent system of equations.

-2x₁ + x₂ - x₃ = 4

x₁ + 2x₂ + 3x₃  = 13

3x₁ + x₃ = -1

Solution

The initial step is to write down the augmented matrix for above system. Keep in mind that coefficients of terms which aren't present are zero.

Here, we want the entries below the main diagonal to be zero. The most main diagonal has been colored red thus we can keep track of it throughout this first illustration.  For reasons which will be apparent eventually we would prefer to find the main diagonal entries to all be ones suitably.

We can find a one in the upper most spot through noticing that if we interchange the first and second row we will find a one in the uppermost spot for free.  Therefore let's do that.

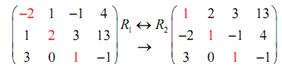
This time we need to find the last two entries as -2 and 3 in the first column to be zero.  We can do this by using the third row operation. Note that if we get 2 times the first row and add this to the second row we will find a zero in the second entry into the first column and if we get -3 times the first row to the third row we will find the 3 to be a zero. We can do both of such operations at similar time so let's do that.

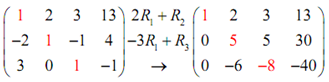
Before proceeding along with the subsequent step, let's ensure that you followed what we just did. Let's see the first operation which we performed. This operation needs to multiply an entry in row 1 with 2 and add it to the consequent entry in row 2 after that replace the old entry in row 2 along with this new entry. The subsequent are the four individual operations which we performed to do this.

2 (1) + (-2) = 0

2 (2) + 1 = 5

2 (3) + (-1) = 5

2 (13) + 4 = 30

Okay, the subsequent step optional, although again is convenient to do. Technically, the 5th element in the second column is okay to leave. Conversely, it will create our life easier down the road if this is a 1. We can utilize the second row operation to support this. We can divide the entire row with 5. Doing it gives,

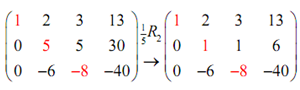
The subsequent step is to then utilize the third row operation to create the -6 in the second column in a zero.

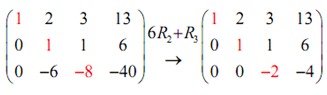
Here, officially we are complete, but again it's somewhat convenient to find all ones on the main diagonal thus we'll do one last step.

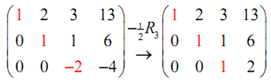
We can now change back to equations.

     x₁ + 2x₂ + 3x₃ = 13

⇒              x₂ + x₃ = 6

                   x₃ = 2

At this point the solving is fairly easy.  We find x₃ for free and once we find that we can plug it in the second equation and find x₂. We can after that use the first equation to find x1. Remember as well that having 1's along the main diagonal helped somewhat along with this process.

The solution to that system of equation is,

x₁ = -1

 x₂  = 4

 x₃  = 2

The process used in this example is termed as Gaussian Elimination.