Solution: We'll require the first and second derivative to do that.

y'(x) = -3/2x^-5/2                                    y''(x) = 15/4x^-7/2

Plug these and also the function in the differential equation.

4x² ((15/4)x^-7/2) + 12((-3/2)x^-5/2) + 3x^-3/2 = 0

(15/4)x^-3/2 -18 x^-3/2 +3x^-3/2 = 0

0 = 0

Thus, y = x^-3/2 does suit the differential equation and therefore is a solution. Why after that did I comprise the condition that x > 0?  I did not use such condition anywhere into the work demonstrating that the function would suit the differential equation.

To see why recall that:

y(x) = x^-3/2 = 1/√x³

In such form this is clear that we will require avoiding x > 0 at the least as that would offer division by zero.

There is also a general rule of thumb which we are going to run along with in such class. This rule of thumb is as: Start along with real numbers, end by real numbers. Conversely, if our differential equation only comprises real numbers so we don't want solutions which provide complex numbers. Thus, in order to ignore complex numbers we will also require avoiding negative values of x.

Thus, we saw in the last illustration that even although a function may symbolically satisfy a differential equation, due to specific restrictions brought about through the solution we cannot utilize all values of the independent variable and thus, must make a restriction on the independent variable. It will be the case with various solutions to differential equations.

In the last illustration, notice that there are in fact several more possible solutions to the differential equation specified.  For example all of the subsequent are also solutions

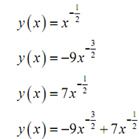
I'll put down the details for you to check that such are actually solutions. Specified these illustrations can you come up along with any other solutions to the differential equation? There are actually an infinite number of solutions to that differential equation.

Thus, given about there are an infinite number of solutions to the differential equation in the last illustration we can ask a natural question. Which is the answer that we want or does that issue which answer we use? This question shows us to the subsequent definition in that section.