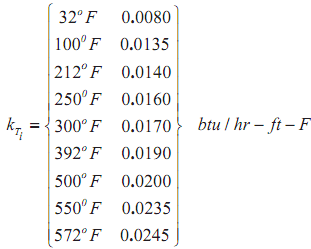Q. Find the shell temperature?

In a shell-and-tube heat exchanger, one fluid passes through a central tube while another fluid flows through an outer shell in the opposite direction. The purpose is to heat the fluid passing through the central tube. It is possible to maintain a constant temperature TS of the outer shell fluid by continually condensing a vapor (for example, steam) along the length of the shell.

By integrating a heat balance equation along the tube, it is possible to relate the length L and diameter D of the heat exchanger to the input temperature T1 and output temperature T₂:

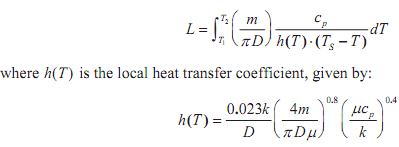
and where

P  = viscosity of the fluid (depends on T)

k  = thermal conductivity of the fluid (depends on T)

c_p  = specific heat of the fluid (depends on T)

m  = flow rate of the fluid through the tube

D  = diameter of the tube

The temperature dependence of the specific heat, viscosity, and thermal conductivity depend on the working fluid and, therefore, upon temperature, T. For this assignment use:

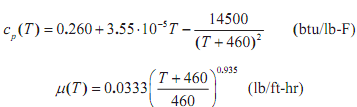
The thermal conductivity data,  () kT , has been evaluated, experimentally, at only a few data (temperature) points.  We have decided, therefore, to use a polynomial approximation and we do so with the full knowledge that our experimental data may contain errors.

where T is measured in degrees Fahrenheit (^oF) throughout.

The Problem:

Given the values of D, m, T₁, T₂, L, determine the necessary shell temperature, T_S. In particular, given that D =1.95 inches (convert to ft), m =25 lb/hr, 170T_F, and the heat exchanger length is L = 5 ft, find the shell temperature T_S needed to heat the output gas to T₂ = 360^oF.