Q. Find the inverse Laplace transform of Y (s) = s-4/s² + 4s + 13 +3s+5/s² - 2s -3.

Q. Use the Laplace transform to solve the initial value problem y''+ y = cos(3t), y(0) = 1, y'(0) = 0.

3. Solve the initial value problem y'' + y = f(t); y(0) = 0; y'(0) = 1;

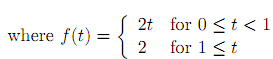
4. Recall from Chapter 4, that initial value problems of the form
ay'' + by'+ cy = f(t); y(0) = y0, y'(0) = y1;

could be used to model the motion of a mass attached to a spring. When the mass is given a sharp blow at time t = p, the forcing function can described using the Dirac delta function δ(t - p). In the special case that p = 0, y0 = 0 and y' (0) = 0, we say:
The solution to the initial value problem

ay''+ by'+ cy = (t); y(0) = 0; y'(0) = 0;

is called the unit impulse response function to the system modeled by the dierential equation.

(a) A mass attached to a spring is in its equilibrium position. After 2 seconds the mass is struck by a hammer exerting an impulse on the mass. The system is modeled by the initial value problem

y''+ y = 4(t   2); y(0) = 0; y'(0) = 0:

Find a function that describes the motion of the mass.

(b) How would the motion change in the last problem if y(0) = 1, i.e., if the mass was released one unit below its equilibrium position at t = 0?