Find out the deflection at mid-span - cantilever beam:

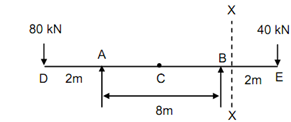
A double overhanging beam of 12 m length rests on supports symmetrically, 8 m apart. A load of 80 kN acts at one free end & a load of 40 kN acts at other free end. Find out the deflection :

 (a) at free ends, and

 (b) at mid-span.

Solution

∑ Fy  = 0, so that R_A + R_B  = 80 + 40 = 120 kN            -------- (1)

Σ M about A = 0,

⇒         R_B  × 8 = 40 × 10 - 80 × 2            -----------(2)

R_B  = 30 kN ( ↑ )

From Eqs. (1) and (2),

R_A  = 90 kN ( ↑ )    ----------(3)

M = - 80 x + 90 [ x - 2] + 30 [ x - 10] ---------- (4)

EI (d ² y/ dx²) = M = - 80 x + 90 [ x - 2] + 30 [ x - 10]            -------- (5)

EI dy/ dx = - 40 x ²+ 45 [ x - 2] ²+ 15 [ x - 10] ²+ C₁           --------- (6)

EIy =- (40 /3)x²  + 15 [ x - 2]³  + 5 [ x - 10]³  + C₁ x + C₂          ----------- (7)

Boundary conditions are following :

At A, x = 2 m, y = 0         --------- (8)

At B, x = 10 m, y = 0      -------- (9)

 From Eqs. (7) and (8),

0 = - (40/3) × 2³ + C1

∴          C₂ =+  320 /3                ---------- (10)

From Eqs. (7), (8) and (9),

0 =( - 40 /3 )× 10³ + 15 [10 - 2]³ + C₁ × 10 +  (320/ 3)

C₁ =+1664 / 3                                ----------- (11)

EIy =- 40 x³  + 15 [ x - 2]³  + 5 [ x - 10]³  + 1664 x + 320      ---------- (12)

Deflection at free ends:

At D,    x = 0

y _D        =+ 320 / 3 EI                               ------- (13)

 At E,    x = 12 m,

EIy   =- (40/3) × 12³ + 15 [12 - 2]³  + 5 [12 - 10]³  + (1664/3) × 12 + (320/3)

∴          y _E        =- 3712/3 EI

Deflection at mid-span :

x = 6 m

EIy C  =- (40 /3)× 63  + 15 [6 - 2]³  + (1664/3) × 6 + (320/3)

y_C  =-   4544/ 3 EI