Q. Explain Fourier Series?
The phasor method of circuit analysis can be extended (by using the principle of superposition) to find the response in linear systems due to nonsinusoidal, periodic source functions. A periodic function (t) with period T can be expressed in Fourier series,
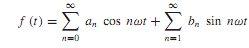
where ω = 2πf = 2π/T is the fundamental angular frequency, a0 is the average ordinate or the dc component of the wave, (a1 cos ωt + b1 sin ωt)isthe fundamental component, and (an cos nωt + bn sin nωt), for n ≥ 2, is the nth harmonic component of the function. The Fourier coefficients are evaluated as follows:

Even though the exact representation of the nonsinusoidal, periodic wave requires an infinite number of terms in the Fourier series, a good approximation for engineering purposes can be obtained with comparatively few first terms, since the amplitude of the harmonics decreases progressively as the order of the harmonic increases.
The systemresponse is determined by the principle of superposition, and the phasor technique yields the steady-state response. Each frequency component of the response is produced by the corresponding harmonic of the excitation. The sum of these responses becomes the Fourier series of the system response. Note that while the phasor method is employed to determine each frequency component, the individual time functions must be used in forming the series for the system response. Such a method of analysis is applicable to all linear systems.